Теория двойственности
Рассмотрим две тесно связанные ЗЛП.
Эти задачи называются симметричными двойственными задачами. Отметим следующие особенности, связывающие эти задачи: 1. Одна из задач является задачей максимизации, а другая – минимизации. 2. В задаче максимизации все неравенства – ≤, а в задаче минимизации – ≥. 3. Число неизвестных одной задачи равно числу неравенств другой. 4. Матрицы коэффициентов при неизвестных в неравенствах обеих задач являются взаимно транспонированными. 5. Свободные члены неравенств одной из задач равны коэффициентам при соответствующих неизвестных в выражении целевой функции другой задачи. Дадим экономическую интерпретацию паре симметричных двойственных задач. Рассмотрим задачу об использовании сырья. Пусть имеется m видов сырья, запасы которых равны b 1, b 2, …, b m. Из этого сырья производят n видов продукции. Расходы сырья i -го вида на производство единицы продукции j -го вида равны a ij. Прибыль от продажи единицы продукции j -го вида равна c j. Найти такой план выпуска продукции, чтобы суммарная прибыль была максимальной. Математической моделью этой задачи является задача 1, где x 1, x 2, …, x n – количество единиц продукции соответствующего вида. Дадим теперь экономическую интерпретацию двойственной задачи. Поставим целью назначить «справедливые» продажные цены на все имеющиеся виды сырья. Пусть y i – цена единицы сырья i -го вида. Потребуем, чтобы продажная цена сырья, необходимого для производства продукции определенного вида, была не меньше выручки, которую можно получить при реализации этой продукции, и рассмотрим задачу минимизации стоимости всего сырья. Математической моделью такой задачи является задача 2. В матричном виде задачи 1 и 2 запишутся следующим образом:
Сформулируем основные теоремы о двойственных задачах. Теорема 2.5. Значение целевой функции задачи максимизации для любого ее плана не превосходит значения целевой функции двойственной к ней задачи минимизации для любого ее плана, т. е. имеет место неравенство:
f (x) ≤ g (y), (2.6)
называемое основным неравенством двойственности. Теорема 2.6. ( достаточное условие оптимальности ). Если для некоторых планов двойственных задач значения целевых функций равны, то эти планы являются оптимальными. Теорема 2.7. ( основная теорема двойственности ). Если ЗЛП имеет конечный оптимум, то двойственная к ней также имеет конечный оптимум, и оптимальные значения целевых функций совпадают. Если целевая функция одной из двойственных задач не ограничена, то условия другой задачи противоречивы. Теорема 2.8. ( о дополняющей нежесткости ). Для того чтобы допустимые решения
Условия (2.7) и (2.8) позволяют, зная оптимальное решение одной из двойственных задач, найти оптимальное решение другой задачи. Рассмотрим экономическую интерпретацию соотношений (2.7) и (2.8). Соотношения (2.7) означают, что если Эта интерпретация позволяет дать ответ на вопрос о целесообразности включения в план нового вида продукции. Пусть новый (n + 1)-й вид продукции характеризуется коэффициентами ai, n +1 затрат i -го ресурса (i = Теорема 2.9. Ценности ресурсов прямой ЗЛП представляет собой значения переменных Действительно, если x * и y * – оптимальные решения соответственно прямой и двойственной ЗЛП, то по основной теореме двойственности Теоремы 2.7, 2.8 и 2.9 называют соответственно первой, второй и третьей теоремами двойственности. Если решать исходную ЗЛП симплекс-методом, то ее нужно привести к ОЗЛП, вводя в каждое ограничение дополнительную переменную. Таким образом, мы получаем соответствие между дополнительными переменными xn + i прямой задачи и переменными yi двойственной задачи ( Теорема 2.10. Компоненты оптимального решения двойственной ЗЛП равны соответствующим элементам индексной строки оптимальной симплекс-таблицы прямой задачи, отвечающим дополнительным переменным. Таким образом, решая симплекс-методом прямую ЗЛП, мы одновременно получаем и решение двойственной задачи. Пример 2.11. ЗЛП, двойственная к модели примера 2.1 имеет следующий вид: g (y 1, y 2, y 3, y 4) = 6 y 1 + 8 y 2 + y 3 + 2 y 4 → min, при ограничениях
Если известно решение исходной задачи (найденное, например, графическим методом)
откуда находим Заметим, что для оптимальных решений Рассмотрим теперь несимметричные двойственные задачи. Если в прямой задаче какое-либо ограничение записано в виде равенства, то соответствующая переменная неограничена в знаке. Действительно, если, например, имеется уравнение a 11 x 1 + a 12 x 2 + … + a 1n x n = b 1, то, записывая его в виде двух неравенств, получим следующие записи симметричных двойственных задач:
Если теперь ввести переменную
Если исходная задача – ОЗЛП, то двойственные задачи записываются в матричном виде следующим образом:
Теоремы 2.5–2.8 остаются справедливыми и для несимметричных двойственных задач.
|

 при ограничениях
при ограничениях
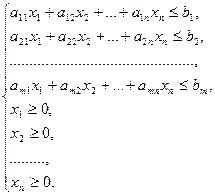
 при ограничениях
при ограничениях

 где с, x Î Rn, b, y Î Rm.
где с, x Î Rn, b, y Î Rm.

 и
и  двойственных задач являлись оптимальными, необходимо и достаточно, чтобы выполнялись следующие соотношения:
двойственных задач являлись оптимальными, необходимо и достаточно, чтобы выполнялись следующие соотношения: (2.7)
(2.7) (2.8)
(2.8) то
то  т. е. если i -й ресурс недефицитен, то его продажная цена должна быть равна нулю. Аналогично, соотношение (2.8) означает, что если выручка
т. е. если i -й ресурс недефицитен, то его продажная цена должна быть равна нулю. Аналогично, соотношение (2.8) означает, что если выручка  от продажи сырья, необходимого для производства единицы продукции j -го вида, больше прибыли c j от продажи этой продукции, то не имеет смысла производить эту продукцию (
от продажи сырья, необходимого для производства единицы продукции j -го вида, больше прибыли c j от продажи этой продукции, то не имеет смысла производить эту продукцию ( ).
). ) и коэффициентом удельной прибыли cn +1. Включение этого вида продукции в оптимальный план задачи на получение максимума прибыли целесообразно, если прибыль, недополученная из-за отвлечения дефицитных ресурсов, т. е.
) и коэффициентом удельной прибыли cn +1. Включение этого вида продукции в оптимальный план задачи на получение максимума прибыли целесообразно, если прибыль, недополученная из-за отвлечения дефицитных ресурсов, т. е.  покрывается полученной прибылью cn +1. Таким образом, если
покрывается полученной прибылью cn +1. Таким образом, если  , то включение в план этого вида продукции выгодно, если же Δ > 0, то невыгодно.
, то включение в план этого вида продукции выгодно, если же Δ > 0, то невыгодно. в оптимальном решении двойственной задачи, т. е.
в оптимальном решении двойственной задачи, т. е.  .
. и
и  .
. ). Из теоремы 2.9 и полученной ранее интерпретации индексной строки оптимальной симплекс-таблицы получаем следующий результат.
). Из теоремы 2.9 и полученной ранее интерпретации индексной строки оптимальной симплекс-таблицы получаем следующий результат.
 то, записывая соотношения (2.7) и (2.8), имеем:
то, записывая соотношения (2.7) и (2.8), имеем:


 и
и  имеет место равенство
имеет место равенство  , которое соответствует теореме 2.7, а компоненты решения
, которое соответствует теореме 2.7, а компоненты решения  совпадают с найденными ранее ценностями ресурсов, что соответствует теореме 2.9. Решение
совпадают с найденными ранее ценностями ресурсов, что соответствует теореме 2.9. Решение 

 то она будет неограничена в знаке, и мы получим запись двойственных задач в несимметричной форме
то она будет неограничена в знаке, и мы получим запись двойственных задач в несимметричной форме