Транспортная задача
Транспортная модель используется для составления наиболее экономичного плана перевозок одного вида продукции (однородного груза) из нескольких пунктов поставки (например, баз или заводов) в пункты потребления (например, заводы или склады). Транспортная задача, по существу, представляет собой задачу линейного программирования, которую можно решать симплекс-методом. Но, в силу особой своей структуры, она допускает решение более простым методом, который по своей сути вытекает из теории двойственности. В простейшей формулировке транспортная задача выглядит следующим образом. Пусть m поставщиков располагают a 1, a 2,..., a m единицами некоторого однородного груза и этот груз должен быть доставлен n потребителям в количествах b 1, b2,..., b n единиц соответственно. Предполагается, что a i > 0, b j > 0. Известны стоимости c ij Пусть xij – количество груза, перевозимого от i -го поставщика j -му потребителю, тогда план перевозок транспортной задачи можно представить в виде матрицы X=(xij) размера минимизировать целевую функцию
при ограничениях
Первая группа ограничений указывает, что суммарный объем перевозок груза от некоторого поставщика должен быть равен имеющемуся у него количеству этого груза. Вторая группа ограничений требует, чтобы суммарные перевозки груза некоторому потребителю удовлетворяли в точности спрос на этот груз. Заметим, что система уравнений (2.10)–(2.11) совместна тогда и только тогда, когда выполняется равенство между суммарными ресурсами и суммарными потребностями:
При выполнении условия (2.13) транспортная модель называется сбалансированной, или закрытой. В противном случае модель называется несбалансированной, или открытой. В реальных условиях не всегда объем предложений равен спросу. Однако транспортную модель всегда можно сбалансировать, т. е. открытая транспортная задача легко может быть сведена к эквивалентной ей закрытой задаче. Если В обоих случаях полученная закрытая транспортная задача будет эквивалентна исходной, т. к. потребности всех реальных потребителей или возможности всех реальных поставщиков останутся прежними, а минимум целевой функции будет достигаться за счет подходящего выбора реальных перевозок, поскольку фиктивные перевозки в целевой функции фактически не фигурируют. Рассмотрим закрытую модель транспортной задачи. Решение транспортной задачи, как и всякой задачи линейного программирования, начинается с нахождения опорного плана. Для транспортной задачи общее число уравнений равно m + n, а число линейно независимых уравнений равно m + n – 1 (сумма первых m уравнений совпадает с суммой последних n). Общее число переменных xij равно mn, число базисных переменных равно m + n – 1, т. е. числу линейно независимых уравнений. Остальные mn – (m + n – 1) = (m – 1)(n – 1) переменных равны нулю и называются свободными переменными. Таким образом, допустимый план будем называть опорным, если в нем отличны от нуля не более m + n – 1 базисных переменных, а остальные переменные равны нулю. Решение транспортной задачи удобно записывать в виде таблицы, имеющей вид матрицы, в которой строки соответствуют пунктам отправления, а столбцы – пунктам потребления. Клеткой (i, j) мы будем называть клетку, стоящую в i -й строке и j -м столбце таблицы. Коэффициенты стоимости cij расположены в правом верхнем углу каждой клетки (i, j). Каждая клетка соответствует паре поставщик-потребитель. Для нахождения исходного опорного решения могут быть использованы различные методы. Рассмотрим некоторые из них.
|

 (
( ) перевозки единицы груза от i -го поставщика j -му потребителю. Следует определить план перевозок, т. е. указать количество груза, которое каждый поставщик должен доставить каждому потребителю, так, чтобы суммарные транспортные затраты были минимальными.
) перевозки единицы груза от i -го поставщика j -му потребителю. Следует определить план перевозок, т. е. указать количество груза, которое каждый поставщик должен доставить каждому потребителю, так, чтобы суммарные транспортные затраты были минимальными. , и математическая модель задачи линейного программирования транспортного типа имеет вид:
, и математическая модель задачи линейного программирования транспортного типа имеет вид: (2.9)
(2.9) ,
,  (2.10)
(2.10)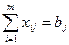 ,
,  (2.11)
(2.11) . (2.12)
. (2.12) . (2.13)
. (2.13) , т. е. имеется избыток продукции по отношению к действительно требуемому ее количеству, то введем в рассмотрение формально еще одного потребителя (фиктивного), с объемом потребностей, равным избытку продукции
, т. е. имеется избыток продукции по отношению к действительно требуемому ее количеству, то введем в рассмотрение формально еще одного потребителя (фиктивного), с объемом потребностей, равным избытку продукции  . Тогда формально имеем закрытую транспортную задачу. Все стоимости перевозок ci, n +1 (
. Тогда формально имеем закрытую транспортную задачу. Все стоимости перевозок ci, n +1 ( ) от каждого поставщика фиктивному потребителю примем равными нулю. Совершенно аналогично можно поступить в случае, когда количество продукции недостаточно для удовлетворения потребностей, т. е.
) от каждого поставщика фиктивному потребителю примем равными нулю. Совершенно аналогично можно поступить в случае, когда количество продукции недостаточно для удовлетворения потребностей, т. е.  . В этом случае вводится фиктивный поставщик с объемом возможных поставок, равным недостатку продукции
. В этом случае вводится фиктивный поставщик с объемом возможных поставок, равным недостатку продукции  . Стоимости перевозок cm+ 1, j (
. Стоимости перевозок cm+ 1, j (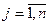 ) от фиктивного поставщика ко всем потребителям принимаем также равными нулю. В первом случае значения фиктивных перевозок x i, n+1 в оптимальном плане будут равны объемам продукции, остающимся у соответствующих поставщиков, во втором случае значения xm +1, j в оптимальном плане будут означать количество продукции, недополученной соответствующим потребителем.
) от фиктивного поставщика ко всем потребителям принимаем также равными нулю. В первом случае значения фиктивных перевозок x i, n+1 в оптимальном плане будут равны объемам продукции, остающимся у соответствующих поставщиков, во втором случае значения xm +1, j в оптимальном плане будут означать количество продукции, недополученной соответствующим потребителем.


