Метод потенциалов
Для формулировки критерия оптимальности используем теоремы двойственности. Выпишем транспортную задачу вместе с двойственной к ней в таблицу 2.9. Для удобства первые m уравнений исходной задачи умножим на –1; неизвестные двойственной задачи, соответствующие первым m уравнениям исходной задачи, обозначены через u 1, u 2, ..., um, а неизвестные, соответствующие последним n уравнениям – через v 1, v2,..., vn. Систему неравенств двойственной задачи кратко можно записать в виде
Неизвестные u 1, u2 ,..., um будем рассматривать как оценки единицы груза, находящегося в распоряжении соответствующего поставщика, или потенциалыпоставщиков, а неизвестные v 1 , v2,..., vm – как оценки единицы груза, доставленного соответствующему потребителю, или потенциалы потребителей. Потенциалы можно интерпретировать соответственно как цены в пункте поставщика или в пункте потребителя. Применяя теорему 2.8 о дополняющей нежесткости, приходим к следующему критерию оптимальности. Таблица 2.9
Окончание таблицы 2.9
Теорема 2.11. (критерий оптимальности плана транспортной задачи). Для того чтобы план перевозок Х* = ( а) для всех базисных клеток плана ( б) для всех свободных клеток ( Замечание. В оба условия критерия потенциалы u i и vj входят только в виде разностей vj – ui, и поэтому потенциалы определяются с точностью до постоянного слагаемого, т. е. если числа Проверим исходное опорное решение Х0, полученное ранее, на оптимальность. С этой целью составим систему уравнений, соответствующих положительным перевозкам (занятым клеткам) плана Х0, т. е. v 1 – u 1 = 2, v 2 – u 2 = 3, v 3 – u 3 = 4, v 2 – u 1 = 4, v 3 – u 2 = 6, v 4– u 3 = 5, где u 1, u 2, u 3 –потенциалы поставщиков, а v 1, v 2, v 3, v 4 – потенциалы потребителей (для удобства эти потенциалы записаны справа и снизу от плана Х0). Решим данную систему, положив, например, u 1 = 0.Получим следующие значения: v 1 = 2, v 2 = 4, u 2 = 1, v 3 = 7, u 3 = 3, v 4 = 8. Для свободных клеток плана Х0 составим систему неравенств:
Подставляя полученные значения потенциалов в данную систему неравенств, имеем:
Неравенства Обозначим разность (vj – ui) – cij= В новом, улучшенном, плане клетка (1, 4) (соответствующая максимуму
Рис. 2.12
Здесь e должно удовлетворять неравенствам
Выбрав наибольшее возможное значение e, т. е. e = 50, получим новый план Х1, представленный на рис. 2.13. Перераспределение перевозок при переходе от плана Х0 к плану Х1 было произведено по замкнутой ломаной линии, называемой обычно циклом (этот цикл отмечен пунктиром на рис. 2.12). Вычислим транспортные затраты для плана Х1
Они оказались меньше транспортных затрат для плана Х0. Следовательно, план Х1 лучше плана Х0. Таким образом, включение в план Х1 перевозки x 14 = 50, оказалось оправданным и транспортные затраты уменьшились на величину
Рис. 2.13
Далее найдем новые значения потенциалов поставщиков и потребителей из уравнений v 1 – u 1 = 2, v 2 – u 2 = 3 v 3 – u 3 = 4, v 4 – u 1 = 3, v 3 – u 2 = 6, v 4 – u 3 = 5, соответствующих занятым клеткам плана Х1. При u 1 = 0 получим v 1 = 2, v 4 = 3, u 3 = –2, v 3 = 2, u 2 = –4, v 2 = –1. Подставив найденные значения потенциалов в неравенства
соответствующие свободным клеткам плана Х1, получим v 2 – u 1 = – 1 < 4, v 1 – u 2 = 6 > 4, v 1 – u 3 = 4 < 6, v 3 – u 1 = 2 < 5, v 4 – u 2 = 7 = 7, v 2 – u 3 = 1 < 5. Не выполняется только третье неравенство, соответствующее перевозке х 21 = 0. В плане Х1 только одна положительная оценка
Рис. 2.14
План Х2 лучше плана Х1, т. к. для него стоимость транспортных затрат v 1– u 1 = 2, v 1 – u 2 = 4, v 3– u 3 = 4, v 4 – u 1 = 3, v 2 – u 2 = 3, v 4 – u 3 = 5 и неравенств
Положив u 1 = 0, из последней системы уравнений получим v 1 = 2, v 4 = 3, u 3 = –2, v 3 = 2, u 2 = –2, v 2 = 1. Найденные значения потенциалов удовлетворяют последней системе неравенств. Действительно,
Так как потенциалы u 1 = 0, v 4 = 3, u 3 = –2, v 1 = 2, v 3 = 2, u 2 = –2, v 2 = 1 удовлетворяют обоим условиям критерия оптимальности, то план Х2 будет оптимальным, а стоимость перевозок f (Х2) = 3600 является минимальной. Оптимальное решение формулируется следующим образом. Первый поставщик должен доставить 150 ед. груза первому потребителю и 100 ед. четвертому, второй поставщик доставит 50 ед. груза первому потребителю и 300 ед. второму и третий поставщик – 350 ед. третьему потребителю и 100 ед. – четвертому. Суммарные транспортные расходы составляют 3600 (денежных единиц). Оптимальный план Х2 выпишем в виде матрицы
Описанный выше метод решения транспортной задачи называется методом потенциалов. Подводя итоги предыдущих рассмотрений, сформулируем последовательность шагов, необходимых для решения транспортной задачи методом потенциалов. Шаг 1. Проверить, является ли данная транспортная задача закрытой. Если да, то перейти ко второму шагу. Если нет, то свести ее к закрытой задаче путем введения либо фиктивного поставщика, либо фиктивного потребителя. Шаг 2. Найти исходное опорное решение (исходный опорный план) закрытой транспортной задачи. Шаг 3. Проверить полученное опорное решение на оптимальность: а) вычислить для него потенциалы поставщиков u iи потребителей v j ; б) для всех свободных клеток (i, j) вычислить оценки в) если все оценки неположительны ( Шаг 4. Выбрать клетку (i*, j*) с наибольшей положительной оценкой и для нее построить замкнутый цикл перераспределения груза. Цикл начинается и заканчивается в выбранной клетке. Получим новое опорное решение, в котором клетка (i*, j*) окажется занятой. Возвращаемся к третьему шагу. Через конечное число шагов будет получено оптимальное решение, т. е. оптимальный план перевозок продукции от поставщиков к потребителям.
|

 (i=
(i=  ; j =
; j =  ).
). где
где 
 где
где 

 ......
......

 ......
......
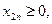

 ...........
...........

 ...........
...........

 ......
......
 ...........
...........



 ....................
....................


 ....................
....................


 ...
...
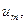

 ,
...
,
...

 любого
знака
любого
знака
 ) был оптимальным, необходимо и достаточно, чтобы существовали числа
) был оптимальным, необходимо и достаточно, чтобы существовали числа 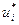 (
(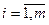 ) и
) и  (
(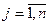 ), удовлетворяющие следующим условиям:
), удовлетворяющие следующим условиям: ;
; и
и 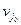 удовлетворяютусловиям критерия, то им будут удовлетворять и числа
удовлетворяютусловиям критерия, то им будут удовлетворять и числа  и
и  , где с – произвольное число.
, где с – произвольное число.






 . Эта величина называется оценкой свободной клетки. Для двух клеток (1, 3) и (1, 4) эти оценки положительны. Выбираем максимальную из них
. Эта величина называется оценкой свободной клетки. Для двух клеток (1, 3) и (1, 4) эти оценки положительны. Выбираем максимальную из них  .
. 50- e
50- e

 250+ e
250+ e



 , т. е.
, т. е.  (чтобы все значения 50 – e, 100 – e, 200 – e были неотрицательными). Для плана Х 1 e стоимость перевозок составит
(чтобы все значения 50 – e, 100 – e, 200 – e были неотрицательными). Для плана Х 1 e стоимость перевозок составит
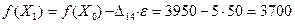 .
. .
.

 . Включая в план Х1 перевозку
. Включая в план Х1 перевозку  , и, перераспределяя другие перевозки по циклу
, и, перераспределяя другие перевозки по циклу  , получим новый план Х2 (см. рис. 2.14)
, получим новый план Х2 (см. рис. 2.14) оказалась меньше, чем для плана Х1. Применительно к плану Х2 вновь составим систему уравнений
оказалась меньше, чем для плана Х1. Применительно к плану Х2 вновь составим систему уравнений




 .
. ;
; ), то решение задачи окончено: исходный опорный план оптимален. Если среди оценок есть хотя бы одна положительная, то переходим к четвертому шагу.
), то решение задачи окончено: исходный опорный план оптимален. Если среди оценок есть хотя бы одна положительная, то переходим к четвертому шагу.


