Нетрадиционные транспортные модели
Использование транспортной модели не ограничивается задачей о транспортировке чего-либо между географическими пунктами отправления и назначения. Транспортную модель можно применять при рассмотрении ряда практических задач, связанных с распределением оборудования, формированием штатного расписания, календарным планированием производства, составлением графика движения транспорта и т. д. Пример 2.13. (задача о распределении оборудования). Пусть на предприятии имеется m видов станков, максимальное время работы которых соответственно равно Для составления математической модели обозначим через xij ( максимизировать целевую функцию
при ограничениях
Эта задача отличается от математической модели транспортной задачи (2.9) – (2.12) только тем, что она является задачей максимизации, а не минимизации. Однако это отличие, как известно, не является существенным: достаточно умножить целевую функцию Пример 2.14. (формирование штатного расписания). Пусть имеются специалисты m профилей в количествах Если ввести матрицу X=(xij), где xij – количество специалистов i -го профиля, выполняющих работу j -го вида, то математическая модель этой задачи, как легко видеть, совпадет с предыдущей. Пример 2.15. Спрос на некоторый скоропортящийся продукт в следующие 4 месяца составляет 400, 300, 420 и 380 тонн соответственно. Предложение этого товара в те же месяцы составляет 500, 600, 200 и 300 тонн. Отпускная цена на этот товар колеблется от месяца к месяцу и равна соответственно 100, 140, 120 и 150 долл. за тонну. Поскольку товар скоропортящийся, он должен быть реализован в течение трех месяцев (включая текущий). Стоимость хранения в течение месяца тонны товара равна 3 долл. Природа товара такова, что невозможна задержка с выполнением заказа. Найти оптимальный план закупки товара. Обозначим xij – количество продукта, закупленного в i -м месяце для потребления в j -м месяце ( минимизировать целевую функцию
Эта модель совпадает с открытой транспортной моделью при дополнительных ограничениях: xij =0 при i> j, x14 =0. Если положить cij =M при i> j, x14 =M, где M – очень большое число, то эти ограничения можно опустить (они будут выполняться автоматически). Остается свести открытую модель к закрытой введением переменных xi5, полагая значения ci5=0. Решение задачи теперь может быть найдено методом потенциалов и имеет вид: x 11 = 400, x 15 = 100, x 22 = 300, x 23 = 220, x 24 = 80, x 33 = 20, x 44 = 300. Значения остальных переменных равны 0. Таким образом, в первый месяц следует закупить 400 тонн продукта, во второй – 600 тонн, из которых 220 тонн предназначены для покрытия спроса третьего месяца и 80 тонн – на покрытие спроса 4-го. В третий месяц следует закупить 200 тонн продукта и в 4-й – 300 тонн. Общая стоимость закупки будет равна 190 540 долл.
|

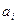 (
(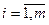 ) часов. Каждый из станков может выполнять n видов операций. Суммарное время выполнения каждой операции соответственно равно bj (
) часов. Каждый из станков может выполнять n видов операций. Суммарное время выполнения каждой операции соответственно равно bj (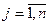 ). Известна производительность cij i -го станка при выполнении j -й операции. Определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей.
). Известна производительность cij i -го станка при выполнении j -й операции. Определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. . Количество деталей, обработанных на всех станках, равно
. Количество деталей, обработанных на всех станках, равно  . Так как максимальное время работы i-го станка ограничено значением
. Так как максимальное время работы i-го станка ограничено значением  если максимальное время работы станков используется полностью, или
если максимальное время работы станков используется полностью, или  если это время используется не полностью. Так как время, отведенное на j -ю операцию, равно bj, то
если это время используется не полностью. Так как время, отведенное на j -ю операцию, равно bj, то 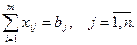 Таким образом, если максимальное время работы используется полностью, мы получаем следующую математическую модель задачи:
Таким образом, если максимальное время работы используется полностью, мы получаем следующую математическую модель задачи:
 ,
, 
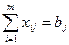 ,
, 
 .
. ). Очевидно, xij =0 при i> j (продукт не может быть потреблен раньше, чем куплен). Кроме того, согласно условию, x14 =0, т. к. продукт должен быть реализован в течение трех месяцев. Пусть cij – затраты на покупку и хранение 1 тонны продукта при покупке в i -м месяце и потреблении в j -м. Тогда c11=100, c22=140, c33=120, c44=150, c12=143, c13=126, c23=123, c24=156, c34=153. Учитывая, что закупки товара в каждом месяце не должны превышать предложения, а потребление в каждом месяце равно спросу, получаем следующую математическую модель:
). Очевидно, xij =0 при i> j (продукт не может быть потреблен раньше, чем куплен). Кроме того, согласно условию, x14 =0, т. к. продукт должен быть реализован в течение трех месяцев. Пусть cij – затраты на покупку и хранение 1 тонны продукта при покупке в i -м месяце и потреблении в j -м. Тогда c11=100, c22=140, c33=120, c44=150, c12=143, c13=126, c23=123, c24=156, c34=153. Учитывая, что закупки товара в каждом месяце не должны превышать предложения, а потребление в каждом месяце равно спросу, получаем следующую математическую модель: при ограничениях
при ограничениях



