Графический метод решения
Графический метод может быть применен, если модель содержит только две переменные. В случае трех переменных этот метод становится менее наглядным, а при большем числе переменных – невозможным. Рассмотрим этот метод на примере конкретной задачи. Пример 2.1. Предприятие изготовляет два вида красок: 1 и 2. Для их производства используются два исходных продукта – А и В. Расходы исходных продуктов и максимальные суточные запасы указаны в таблице.
Изучение рынка сбыта показало, что суточный спрос на 2-ю краску не превышает спроса на первую краску более чем на 1 т. Кроме того, установлено, что спрос на 2-ю краску никогда не превышает 2 т в сутки. Цены 1 т красок равны: 3 у. е. для 1-й краски и 2 у. е. для 2-й краски. Какое количество краски каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
Согласно условиям задачи, должны выполняться следующие ограничения:
Изобразим на координатной плоскости область допустимых решений. Множество решений каждого из неравенств есть полуплоскость, на которую указывает стрелка (рис. 2.1). Граница полуплоскости (прямая) задается соответствующим уравнением (когда знак неравенства заменяется знаком равенства). Полученная таким образом допустимая область – многоугольник OABCDE. Необходимо среди точек этого многоугольника найти точку, в которой целевая функция f принимает максимальное значение.
Решая систему, находим
Рассмотрим еще несколько примеров, в которых возникают особые случаи решения ЗЛП. При этом мы не будем приводить конкретную задачу, а сразу будем рассматривать математическую модель. Пример 2.2. (Бесконечное множество решений). Максимизировать
Рис. 2.3
Как видно из рис. 2.3, линии уровня Пример 2.3. (Неограниченная целевая функция).
Рис. 2.4
Из рис. 2.4 видно, что задача не имеет оптимального решения, т. к. допустимая область не ограничена в направлении возрастания целевой функции. Характеризуя такую ситуацию, говорят, что и допустимая область, и оптимальное значение целевой функции не ограничены. Неограниченность решения ЗЛП свидетельствует о том, что разработанная модель недостаточно точна. Отметим наиболее типичные возможные ошибки: · не учтено одно или несколько ограничений; · неточно оценены параметры (постоянные), фигурирующие в некоторых ограничениях. Пример 2.4. (Отсутствие допустимых решений).
Рис. 2.5
Задача не имеет решения, т. к. множество планов этой задачи пусто (система ограничений несовместна). С практической точки зрения отсутствие допустимых решений следует рассматривать как свидетельство того, что модель построена некорректно, т. к. введенные ограничения оказались противоречивыми. После того как оптимальное решение получено, представляет интерес анализ модели на чувствительность. Для формулировки основных задач такого анализа введем необходимые определения. Определение 2.2. Ограничение называется связывающим, если соответствующая ему прямая проходит через оптимальную точку, в противном случае – несвязывающим. Ресурс, соответствующий связывающему ограничению, называется дефицитным, а соответствующий несвязывающему ограничению – недефицитным. Ресурс называется избыточным, если исключение соответствующего ему ограничения не изменяет не только оптимального решения (как в случае недефицитного ресурса), но и допустимой области. Рассмотрим основные задачи анализа модели на чувствительность и проиллюстрируем их на примере 1. 1. Каково предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение?
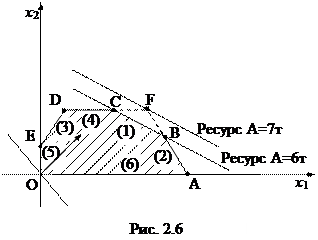
Из рис. 2.6 видно, что при увеличении запаса ресурса А прямая (1) перемещается параллельно вверх, постепенно стягивая в точку треугольник BCF. При этом точка оптимума движется от B к F и увеличивается значение целевой функции. При запасе ресурса А = 7 т областью допустимых решений является многоугольник OAFDE, ограничения (2) и (4) становятся связывающими. Дальнейшее увеличение запаса ресурса А делает его избыточным. На рис. 2.7 аналогично можно проследить увеличение запаса ресурса В.
Рис. 2.7
2. Каково предельно допустимое снижение запаса недефицитного ресурса, не изменяющее найденного ранее оптимального значения целевой функции? Из рис. 2.6 видно, что прямую (4) можно опускать до пересечения с точкой оптимума В без изменения оптимального решения, т. е. спрос на краску 2 может быть снижен до 1⅓ без изменения оптимума. Аналогично, прямую (3) можно двигать вниз пока она не достигнет точки В. При этом правая часть ограничения (3) станет равной Таблица 2.1
3. Увеличение объема какого из ресурсов наиболее выгодно? Для ответа на этот вопрос вводится понятие ценности уi дополнительной единицы
где Ценности ресурсов в экономике называют также теневыми ценами или скрытыми ценами, или объективно обусловленными оценками. Заметим, что их нельзя отождествлять с действительными ценами, по которым возможна закупка соответствующих ресурсов. Здесь имеется в виду некоторая мера, характеризующая ценность ресурса только относительного полученного оптимального решения. Из таблицы 2.1 получаем: у 1 = 4. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения? На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?
При При
|

 Решение. Пусть x 1, x 2 – количества 1-й и 2-й краски соответственно (в тоннах), производимых предприятием. Тогда доход от реализации f (x 1, x 2) = 3 x 1 + 2 x 2.
Решение. Пусть x 1, x 2 – количества 1-й и 2-й краски соответственно (в тоннах), производимых предприятием. Тогда доход от реализации f (x 1, x 2) = 3 x 1 + 2 x 2.

 Рассмотрим так называемую линию уровня функции f, т. е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение с, т. е. f (x 1, x 2) =c. В данном случае линия уровня
Рассмотрим так называемую линию уровня функции f, т. е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение с, т. е. f (x 1, x 2) =c. В данном случае линия уровня  есть прямая. При различных уровнях с линии уровня параллельны. На рис. 2.2 изображены три линии уровня. Одна из них проходит через начало координат и соответствует значению с = 0. Как известно из аналитической геометрии, вектор нормали
есть прямая. При различных уровнях с линии уровня параллельны. На рис. 2.2 изображены три линии уровня. Одна из них проходит через начало координат и соответствует значению с = 0. Как известно из аналитической геометрии, вектор нормали  показывает направление возрастания уровня. Следовательно, оптимальное решение достигается в точке B (это точка допустимой области, соответствующая максимальному значению с). Точка В есть точка пересечения прямых (1) и (2) и поэтому ее координаты определяются из решения системы уравнений
показывает направление возрастания уровня. Следовательно, оптимальное решение достигается в точке B (это точка допустимой области, соответствующая максимальному значению с). Точка В есть точка пересечения прямых (1) и (2) и поэтому ее координаты определяются из решения системы уравнений
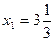 ,
,  . Оптимальный доход при этом составит
. Оптимальный доход при этом составит (у. е.).
(у. е.). при ограничениях
при ограничениях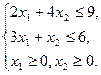


 параллельны прямой (2), имеющей уравнение
параллельны прямой (2), имеющей уравнение  . Следовательно, задача имеет бесконечное множество оптимальных решений. Такими решениями являются координаты любой из точек отрезка АВ. Целевая функция имеет в каждой точке этого отрезка одно и то же (максимальное) значение, равное 12. Такие решения называются альтернативными оптимальными решениями. Информация о наличии альтернативных оптимумов оказывается очень полезной при решении практических задач, т. к. лицо, принимающее решение, получает возможность выбора альтернативного варианта, наиболее отвечающего сложившейся ситуации, и при этом не нужно исследовать изменения целевой функции.
. Следовательно, задача имеет бесконечное множество оптимальных решений. Такими решениями являются координаты любой из точек отрезка АВ. Целевая функция имеет в каждой точке этого отрезка одно и то же (максимальное) значение, равное 12. Такие решения называются альтернативными оптимальными решениями. Информация о наличии альтернативных оптимумов оказывается очень полезной при решении практических задач, т. к. лицо, принимающее решение, получает возможность выбора альтернативного варианта, наиболее отвечающего сложившейся ситуации, и при этом не нужно исследовать изменения целевой функции.





 В примере 1 связывающими являются ограничения (1) и (2). Им соответствуют запасы исходных продуктов (ресурсов) А и В, которые, следовательно, являются дефицитными.
В примере 1 связывающими являются ограничения (1) и (2). Им соответствуют запасы исходных продуктов (ресурсов) А и В, которые, следовательно, являются дефицитными.
 . Результаты анализа представим в табл. 2.1.
. Результаты анализа представим в табл. 2.1. ,
, − максимальное приращение оптимального значения целевой функции,
− максимальное приращение оптимального значения целевой функции,  максимально допустимый прирост i -го ресурса.
максимально допустимый прирост i -го ресурса.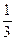 , у 2 =
, у 2 = 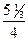 =
=  , у 3 = 0, у 4 = 0. Таким образом, более выгодным является увеличение ресурса В.
, у 3 = 0, у 4 = 0. Таким образом, более выгодным является увеличение ресурса В. Обозначим c 1 и c 2 цены на краски 1 и 2 соответственно. Из рис. 2.8 видно, что при увеличении c 1 или уменьшении c 2 прямая
Обозначим c 1 и c 2 цены на краски 1 и 2 соответственно. Из рис. 2.8 видно, что при увеличении c 1 или уменьшении c 2 прямая  (линия уровня целевой функции) вращается по часовой стрелке, а при уменьшении c1 и увеличении c 2 – против. Это легко проследить на соответствующем повороте вектора нормали к этой прямой, имеющего, как известно, координаты (c 1, c 2). Если меняются оба коэффициента c 1 и c 2 одновременно, то поворот линии уровня определится отношением c 1/ c 2. Точка В будет оставаться оптимальной при условии, что наклон прямой
(линия уровня целевой функции) вращается по часовой стрелке, а при уменьшении c1 и увеличении c 2 – против. Это легко проследить на соответствующем повороте вектора нормали к этой прямой, имеющего, как известно, координаты (c 1, c 2). Если меняются оба коэффициента c 1 и c 2 одновременно, то поворот линии уровня определится отношением c 1/ c 2. Точка В будет оставаться оптимальной при условии, что наклон прямой  .
. получим альтернативный оптимум с отрезком ВС в качестве множества оптимальных точек. Аналогично при
получим альтернативный оптимум с отрезком ВС в качестве множества оптимальных точек. Аналогично при  имеем альтернативный оптимум – отрезок АВ.
имеем альтернативный оптимум – отрезок АВ. оптимум перемещается в точку А и ресурс 1 перестает быть дефицитным. При
оптимум перемещается в точку А и ресурс 1 перестает быть дефицитным. При  оптимум перемещается в точку С и становится дефицитным ресурс 4, а ресурс 2 перестает быть таковым.
оптимум перемещается в точку С и становится дефицитным ресурс 4, а ресурс 2 перестает быть таковым.


