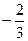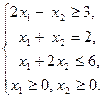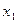Симплекс-метод
Наиболее популярным универсальным алгебраическим методом решения ЗЛП является симплекс-метод, разработанный американским ученым Дж. Данцигом в 1949 г. [1] Для того чтобы понять суть этого метода, рассмотрим сначала его геометрическую интерпретацию. Напомним определение выпуклого множества, играющего важную роль в линейном программировании. Определение 2.3. Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки. Согласно этому определению, фигуры а и б на рис. 2.9 являются выпуклыми, а фигуры в и г – не являются таковыми.
Рис. 2.9
Как легко видеть, пересечение любого числа выпуклых множеств является выпуклым множеством. Как мы видели в п. 2.2, в случае двух переменных множество решений линейного неравенства (уравнения) представляет собой полуплоскость (прямую). Пересечение этих полуплоскостей (и прямых, если в системе ограничений есть уравнения) представляет собой допустимую область. Если она не пуста, то является выпуклым множеством и называется многоугольником решений. Это может быть точка, отрезок, луч, многоугольник или неограниченная многоугольная область. В случае трех переменных допустимая область ЗЛП есть пересечение полупространств и, возможно, плоскостей, и называется многогранником решений. Множество точек, в которых целевая функция принимает фиксированное значение, образует поверхность уровня, которая в данном случае является плоскостью. Следовательно, если решение существует, то точкой оптимума является одна из вершин многогранника решений (или вся грань – в случае альтернативного оптимума). Аналогично, при n > 3 каждое неравенство аi 1 x 1 + аi 2 x 2 + …+ аinxn ≤ bi, i = Геометрическая интерпретация симплекс-метода состоит в следующем: 1. Выбирается произвольная вершина многогранника решений. Соответствующее ей допустимое решение, необязательно оптимальное, называется начальным опорным решением. 2. От исходной вершины осуществляется переход к смежной вершине с лучшим значением целевой функции. Полученное решение проверяется на оптимальность с помощью критерия оптимальности. Процесс повторяется до тех пор, пока не будет найдено оптимальное решение, либо будет установлено его отсутствие (неограниченность целевой функции на множестве планов). Для описания алгоритма симплекс-метода нам потребуется ряд определений. Определение 2.4. Система линейных уравнений называется системой с базисом, если в каждом уравнении содержится неизвестное с коэффициентом, равным 1, отсутствующее в остальных уравнениях системы. Эти неизвестные называются базисными, остальные – свободными. Система с базисом имеет вид:
где р + m = n, т. е. p = n – m. Система (2.3) всегда имеет решение (0, 0, Определение 2.5. Систему линейных уравнений будем называть канонической, если она является системой с базисом и все bi ≥ 0. Базисное решение в этом случае оказывается планом, т. к. его компоненты неотрицательны. Назовем его базисным (или опорным) планом канонической системы. Определение 2.6. ОЗЛП будем называть канонической (КЗЛП) [2], если система линейных уравнений этой задачи – каноническая, а целевая функция выражена только через свободные неизвестные. Пример 2.5. Рассмотрим систему ограничений ЗЛП из примера 2.1. Вводя дополнительные переменные, приведем ее к системе уравнений
при условии неотрицательности переменных xi (i = Эта система является канонической, переменные x 3, x 4, x 5, x 6 являются базисными, а переменные x 1, x 2 – свободными. Так как целевая функция f(x 1, x 2 ) = 3 x 1 + 2 x 2 выражена через свободные неизвестные, то мы получили КЗЛП. Решение КЗЛП симплекс-методом удобно записывать в виде симплекс-таблиц.
f(x 1,
на множестве планов канонической линейной системы (2.3). Этой задаче соответствует следующая симплекс-таблица. Таблица 2.2
Последняя строка этой таблицы называется индексной. Она соответствует уравнению с 1 x 1 + c 2 x 2 + Сформулируем теперь ряд теорем, которые лежат в основе симплекс-метода. Для определенности будем рассматривать задачу максимизации. Теорема 2.1. Если в симплекс-таблице среди коэффициентов при каком-либо свободном неизвестном имеется хотя бы один положительный элемент, то возможен переход к новой канонической задаче, равносильной исходной, в которой указанное свободное неизвестное оказывается базисным (при этом одно из базисных неизвестных переходит в число свободных). Доказательство. Пусть, например, среди коэффициентов при x 1 есть положительные и
Таблица 2.3
Теперь х 1 – базисное неизвестное, а хр +1 – свободное. В последнем столбце все элементы положительны, т. е. табл. 2.3 соответствует канонической задаче. Действительно, для неположительных аi1 (i = Теорема 2.2. (об улучшении базисного плана). Если в индексной строке симплекс-таблицы задачи максимизации содержится отрицательный элемент сj, а в столбце хj имеется хотя бы один положительный элемент, причем ключевое отношение Доказательство. Пусть, например, с1 < 0 и а 11 > 0 – ключевой элемент. Тогда переход от таблицы 1 к таблице 2 меняет значение целевой функции с с 0 на Теорема 2.3. (достаточное условие оптимальности). Если все элементы индексной строки симплекс-таблицы задачи максимизации неотрицательны, то базисный план этой задачи является оптимальным, а с0 есть максимум целевой функции на множестве планов задачи. Доказательство. Пусть xb = (0, …, 0, b 1, …, bm) – базисный план. Тогда f (xb) = c 0. Если Теорема 2.4. (случай неограниченности целевой функции). Если в индексной строке симплекс-таблицы задачи максимизации содержится отрицательный элемент сj, а в столбце неизвестного хj все элементы неположительны, то на множестве планов задачи целевая функция не ограничена сверху. Доказательство. Пусть, например, с 1 < 0 и аi 1 ≤ 0 при i = Рассмотрим вектор x θ = (θ, 0, …, 0, b 1- a 11 θ, …, bm – am 1 θ). Легко проверить подстановкой, что Теоремы 2.1–2.4 позволяют сформулировать алгоритм симплекс-метода для задачи максимизации КЗЛП. 1. Записываем данную КЗЛП в исходную симплекс-таблицу. 2. Если все элементы индексной строки симплекс-таблицы неотрицательны, то базисный план задачи является оптимальным (теорема 2.3). 3. Если в индексной строке содержится отрицательный элемент, над которым в таблице нет ни одного положительного, то целевая функция не ограничена сверху на множестве планов и задача не имеет решений (теорема 2.4). 4. Если над каждым отрицательным элементом индексной строки имеется в таблице хотя бы один положительный, то следует перейти к новой симплекс-таблице, для которой базисный план не хуже предыдущего (теорема 2.2). С этой целью (см. доказательство теоремы 2.1): а) выбираем в таблице ключевой столбец, в основании которого находится какой-либо отрицательный элемент индексной строки; б) выделяем ключевое отношение (минимальное из отношений bi к положительным элементам ключевого столбца), знаменатель которого будет ключевым элементом; в) составляем новую симплекс-таблицу; для этого делим ключевую строку (строку, в которой находится ключевой элемент) на ключевой элемент, а затем из всех остальных строк (включая индексную) вычитаем полученную строку, умноженную на соответствующий элемент ключевого столбца (чтобы все элементы этого столбца, кроме ключевого, стали равны 0). 5. При рассмотрении полученной симплекс-таблицы непременно представится один из трех случаев, описанных в пп. 2, 3, 4. Если при этом возникнут ситуации пп. 2 или 3, то процесс решения задачи завершается, если же возникнет ситуация п. 4, то процесс продолжается. Если учесть, что число различных базисных планов конечно, то возможны два случая: а) через конечное число шагов задача будет решена (возникнут ситуации пп. 2 или 3); б) начиная с некоторого шага возникает зацикливание (периодическое повторение симплексных таблиц и базисных планов). Сразу отметим, что зацикливание при решении задач симплекс-методом практически не встречается и имеется лишь несколько искусственных примеров зацикливания, построенных с большим трудом. По этой причине мы не будем рассматривать приемы, позволяющие избежать зацикливания. Замечание. Выбор ключевого столбца (см. п. 4а), вообще говоря, произволен. Однако на практике удобно руководствоваться определенным правилам. Одним из таких эвристических правил является следующее: в качестве ключевого столбца выбирается тот, который отвечает наибольшему по модулю отрицательному элементу индексной строки. Пример 2.6. Решим симплекс-методом КЗЛП из примера 2.5. При этом добавим в симплекс-таблицу столбец, в который будем записывать отношения bi к положительным элементам ключевого столбца. Таблица 2.4
Последняя симплекс-таблица соответствует оптимальному решению, т. к. в индексной строке нет отрицательных элементов. Рассмотрим ее интерпретацию. Столбец значений дает нам оптимальное решение: Таким образом, часть ответов на вопросы анализа модели на чувствительность непосредственно представлена в конечной симплекс-таблице. Для ответов на остальные вопросы необходимо проделать небольшие вычисления. Определим интервал значений изменения какого-либо ресурса (например, 1-го), при котором его теневая цена остается неизменной. Увеличение запаса ресурса 1 на величину Δ соответствует замене переменной х 3 в системе (2.4) на х 3 – Δ. Делая ту же замену в последней симплекс-таблице, а затем перенося Δ в правую часть, получим столбец значений переменных:
Решая эту систему, находим Определим теперь интервалы изменений коэффициентов целевой функции, при которых не происходит изменения оптимального решения. Пусть целевая функция имеет вид
Так как из последней симплекс-таблицы имеем
т. е. новая индексная строка получается прибавлением к старой индексной строке строки, отвечающей x 1, умноженной на Δ. Для того чтобы найденная точка оптимума для f осталась точкой оптимума для f *, нужно выполнение условий:
т. е. –2≤ Δ ≤ 1. Отсюда находим пределы изменения коэффициента c 1 при x 1 в целевой функции: 1≤ c 1 ≤ 4 (т. к. c 1 = 3 + Δ). Аналогично находится интервал изменения коэффициента при x 2. Пример 2.7. Решим симплекс-методом задачу примера 2.2. Вводя дополнительные переменные, приведем ее к ОЗЛП, которая будет и канонической: f (x 1, x 2) = 6 x 1 + 2 x 2 → max,
Таблица 2.5
Последняя симплекс-таблица является оптимальной. Ей отвечает оптимальное решение x 1 = 2, x 2 = 0, f max = 12. Это решение соответствует точке А на рис. 2.3. Нулевое значение коэффициента при свободной переменной x 2 в индексной строке говорит о наличии альтернативного оптимума. Мы можем вывести переменную x 3 из базиса, введя вместо нее переменную x 2. При этом значение целевой функции не изменяется, но мы получим другое оптимальное решение (соответствующее точке В). Пример 2.8. Решим симплекс-методом задачу примера 2.3, которая после введения дополнительных переменных принимает вид: f (x 1, x 2) = x 1 + x 2 → max,
Мы получили систему с базисными переменными x 1 и x 4. Выразим целевую функцию через свободные переменные, найдя x 1 = 1 + x 2 + x 3 из первого уравнения системы: f = 1 + 2 x 2 + x 3. Полученную КЗЛП запишем в симплекс-таблицу:
Так как в индексной строке имеется отрицательный элемент (–1), а в соответствующем ему столбце все элементы неположительны, то по теореме 2.4 целевая функция неограничена сверху, т. е. задача не имеет решения.
Мы рассмотрели алгоритм симплекс-метода применительно к КЗЛП. Однако не любая ОЗЛП является канонической. В таком случае от ОЗЛП переходят к канонической путем добавления искусственных переменных в каждое из уравнений системы, в котором отсутствует базисное неизвестное (предполагаем, что все b i ≥ 0). В целевую функцию исходной задачи добавляется в случае максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число. К полученной КЗЛП применяется симплекс-метод. При этом следует вычеркивать в симплекс-таблице искусственные переменные по мере их перехода в свободные. Если оптимальное решение содержит искусственные переменные в качестве базисных или задача неразрешима, то исходная задача также неразрешима. В противном случае мы получаем оптимальное решение исходной задачи. Описанный выше метод называется М-методом или методом больших штрафов. Пример 2.9. Найти минимум целевой функции f (x 1, x 2) = 3 x 1 – 2 x 2 при условиях:
Вводя дополнительные переменные и переходя к задаче на максимум, приведем исходную задачу к ОЗЛП: g (x 1, x 2) = –3 x 1 + 2 x 2 → max,
Базисная переменная имеется только в последнем уравнении. Для приведения к КЗЛП введем искусственные переменные y 1, y 2:
h (x, y) = –3 x 1 + 2 x 2 – M (y 1 + y 2) → max. Выражая y 1 и y 2 из соответствующих уравнений системы и подставляя в выражение для h, получим h = – 3 x1 + 2 x2 – M( 3 – 2 x1 + x2 + x3) –M ( 2 – x1 – x2 + x4) = – 5 M + (3 M –3) x 1 + 2 x 2 – Таблица 2.6
Продолжение таблицы 2.6
Следовательно, f min = 3, 6 при x 1 = 2, 4, x 2 = 1, 8.
Пример 2.10. Приведем модель из примера 2.4 к КЗЛП и решим ее симплекс-методом.
g = –2 x 1 – 3 x 2 – My 1 → max. Выражая y 1 из первого уравнения, получим g = (M – 2) x 1 + (М – 3) x 2 – Mx 3 – 10 М.
Таблица 2.7
Получили оптимальную симплекс-таблицу, содержащую искусственную переменную y 1 в качестве базисной. Следовательно, исходная задача неразрешима (допустимая область пуста).
|


 , определяет полупространство n- мерного пространства (в случае уравнения – гиперплоскость). Их пересечение также называют многогранником решений, и оно является выпуклым множеством.
, определяет полупространство n- мерного пространства (в случае уравнения – гиперплоскость). Их пересечение также называют многогранником решений, и оно является выпуклым множеством. (2.3)
(2.3) , 0, b 1, b 2,
, 0, b 1, b 2,  (2.4)
(2.4) ).
). хn
хn
 .
.  называется ключевым отношением. Пусть, например,
называется ключевым отношением. Пусть, например,  . Элемент а 11 называется тогда ключевым элементом. Используя метод Гаусса, исключим неизвестное х 1 из всех уравнений, кроме первого. Для этого разделим первую строку на а 11, а затем вычтем из каждой i -й строки первую, умноженную на аi 1 (i =
. Элемент а 11 называется тогда ключевым элементом. Используя метод Гаусса, исключим неизвестное х 1 из всех уравнений, кроме первого. Для этого разделим первую строку на а 11, а затем вычтем из каждой i -й строки первую, умноженную на аi 1 (i =  ). Из индексной строки также вычтем первую, умноженную на с 1. Получим следующую симплекс-таблицу:
). Из индексной строки также вычтем первую, умноженную на с 1. Получим следующую симплекс-таблицу:








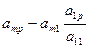


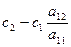



 . Для положительных аi1 это следует из выбора
. Для положительных аi1 это следует из выбора 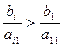 и, следовательно,
и, следовательно,  , (i =
, (i =  , т. к. с 1 < 0,
, т. к. с 1 < 0,  .
. . Теорема доказана.
. Теорема доказана. θ
θ  R xθ – решение системы (2.3). При θ > 0 это решение допустимое, т. к. bi – ai 1 θ ≥ 0 при i =
R xθ – решение системы (2.3). При θ > 0 это решение допустимое, т. к. bi – ai 1 θ ≥ 0 при i = 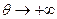 . Теорема доказана.
. Теорема доказана.
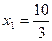 ,
, 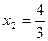 и максимальное значение целевой функции
и максимальное значение целевой функции  . Значения переменных x 5 = 3 и
. Значения переменных x 5 = 3 и  дают нам остатки ресурсов 3 и 4 (дополнительные переменные x 5 и x 6 соответствуют этим ресурсам), т. е. эти ресурсы являются недефицитными, и их запасы могут быть снижены на указанные значения без изменения оптимального решения (ср. табл. 2.1). Переменные x 3 и x 4 являются свободными, т. е. x 3 = x 4 = 0, и, соответственно, ресурсы 1 и 2 являются дефицитными. Индексная строка дает выражение для целевой функции:
дают нам остатки ресурсов 3 и 4 (дополнительные переменные x 5 и x 6 соответствуют этим ресурсам), т. е. эти ресурсы являются недефицитными, и их запасы могут быть снижены на указанные значения без изменения оптимального решения (ср. табл. 2.1). Переменные x 3 и x 4 являются свободными, т. е. x 3 = x 4 = 0, и, соответственно, ресурсы 1 и 2 являются дефицитными. Индексная строка дает выражение для целевой функции:  , откуда находим
, откуда находим  ,
,  . Из уравнений системы (2.4) следует, что увеличение x 3 и x 4 эквивалентны соответственно снижению запасов ресурсов 1 и 2. Поэтому коэффициенты 1/3 и 4/3 представляют собой ценности ресурсов 1 и 2 соответственно. Ценности ресурсов 3 и 4 равны 0, как видно из этой же индексной строки. Это и естественно, т. к. они недефицитные.
. Из уравнений системы (2.4) следует, что увеличение x 3 и x 4 эквивалентны соответственно снижению запасов ресурсов 1 и 2. Поэтому коэффициенты 1/3 и 4/3 представляют собой ценности ресурсов 1 и 2 соответственно. Ценности ресурсов 3 и 4 равны 0, как видно из этой же индексной строки. Это и естественно, т. к. они недефицитные. . Для того чтобы это решение было оптимальным, необходимо и достаточно, чтобы оно было допустимым, т. е.
. Для того чтобы это решение было оптимальным, необходимо и достаточно, чтобы оно было допустимым, т. е.
 . Аналогично находятся интервалы изменений запасов остальных ресурсов.
. Аналогично находятся интервалы изменений запасов остальных ресурсов.
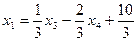 ,
,  ,
,