Целочисленное линейное программирование
Задачи линейного программирования, в которых все или некоторые переменные должны удовлетворять условиям целочисленности, называются задачами целочисленного (или диофантового, или дискретного)линейного программирования (ЗЦЛП). Задача называется полностью целочисленной, если все переменные должны удовлетворять условию целочисленности, и частично целочисленной, если это условие накладывается только на некоторые переменные. В ряде экономических задач условие целочисленности возникает естественным образом, например, если некоторая переменная представляет собой количество единиц неделимой продукции (станки, автомобили, телевизоры и т. п.). Однако в некоторых задачах целочисленные переменные не являются ярко выраженными и вводятся искусственно. Пример 2.16. Пусть имеется n видов промышленной продукции. Затраты на производство продукции i -го вида складываются из постоянных затрат bi и издержек аi на производство единицы продукции. Если хi – объем выпуска продукции i -го вида, то функция затрат на производство этого вида продукции имеет вид
Целевой функцией является функция суммарных затрат Пусть Тогда Итак, получаем следующую математическую модель искомой задачи:
при ограничениях
Переменные, принимающие два значения: 0 или 1, называются булевыми. Таким образом, мы получили частично-целочисленную задачу с булевыми переменными. При этом булевы переменные К задачам ЦЛП сводится и ряд специальных задач. Одной из них является задача о назначениях. Она может быть сформулирована следующим образом. Требуется распределить n работ (или исполнителей) по n станкам. Выполнение i -й работы на j -м станке связано с затратами cij. Задача состоит в таком распределении работ по станкам (одна работа выполняется одним станком), которое соответствует минимуму суммарных затрат. Введем переменные
Требуется найти матрицу Х = (
при ограничениях
где Ограничения (2.15) означают, что каждая работа выполняется на одном станке, а ограничения (2.16) означают, что каждый станок выполняет одну работу. Другой задачей подобного рода является задача о коммивояжере, которая может быть сформулирована следующим образом. Имеется n городов, пронумерованных числами от 1 до n. Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Известны расстояния между городами dij К задачам целочисленного программирования приводят также многие оптимальные задачи теории расписаний, в которой рассматриваются методы оптимизации оперативно-календарного планирования. Отметим, что задача о назначениях является частным случаем транспортной задачи, а решение транспортной задачи всегда является целочисленным (при целочисленности ограничений). Однако в общем случае условие целочисленности решения не выполняется автоматически. В ряде случаев ЗЦЛП решают обычным методом, например симплекс-методом, с последующим округлением до целых чисел. Такой подход оправдан, когда отдельная единица составляет очень малую часть всего объема. В противном случае такое округление может привести к плану, существенно отличающемуся от оптимального, или вообще вывести за пределы множества планов. Поэтому разработаны специальные методы решения ЗЦЛП, среди которых можно выделить две основные группы: методы отсечения и комбинаторные методы. Одним из наиболее популярных методов отсечения является метод Гомори. Он основан на симплекс-методе и состоит в следующем: 1. Симплекс-методом находят оптимальный план. Если он целочисленный, то вычисления заканчивают. 2. Если оптимальный план содержит хотя бы одну дробную компоненту, то накладывают дополнительное линейное ограничение, учитывающее целочисленность компонент плана, и переходят к п. (1). В результате либо будет найден оптимальный целочисленный план, либо доказано, что задача не имеет целочисленных планов. Геометрически добавление линейного ограничения отвечает проведению плоскости, которая отсекает от многогранника решений некоторую его часть вместе с оптимальной точкой с нецелыми координатами, но оставляет все целочисленные точки многогранника решений. Опишем процесс составления нового ограничения в случае полностью целочисленной ЗЛП. Пусть оптимальная симплекс-таблица имеет вид табл. 2.2 и пусть, например,
В этом уравнении левая часть < 1, т. к. {
Это неравенство и определяет дополнительное ограничение, которое называется отсечением Гомори для полностью целочисленной задачи. Полученное ранее решение не удовлетворяет этому ограничению, т. к. в этом решении Пример 2.14. Рассмотрим модель из примера 2.1 при дополнительном условии целочисленности переменных х 1 и х 2 (например, краска выпускается цистернами по 1 т). Тогда и дополнительные переменные будут целочисленными. Рассмотрим уравнение, отвечающее первой строке оптимальной симплекс-таблицы из примера 2.6:
Записывая это уравнение в виде
приходим к выводу, что
Это и есть одно из дополнительных ограничений, порождаемых условием целочисленности. Исходя из 2-го или 4-го уравнений, можно было бы получить и другие ограничения. Для частично целочисленной ЗЛП из уравнения (2.17) не следует неравенство (2.18), т. к. правая часть уже не обязана быть целой. Однако можно построить отсечение другого типа, более сложное, которое мы здесь рассматривать не будем. Представление о комбинаторных методах дает широко используемый на практике метод ветвей и границ. Он применим как к полностью, так и к частично целочисленным ЗЛП. Алгоритм этого метода следующий. Решается ослабленная задача (ЗЛП без условий целочисленности). Если найденное решение удовлетворяет накладываемым условиям целочисленности, то решение – оптимальное. Если хr – целочисленная переменная, значение которой Каждая из полученных подзадач также решается как ЗЛП. Если найденный оптимум будет допустимым для целочисленной задачи, то он фиксируется как наилучший, и ветвление этой подзадачи заканчивается. Если будет найдено целочисленное решение какой-либо из подзадач, лучшее имеющегося, то оно фиксируется в качестве наилучшего. Если оптимальное решение ослабленной подзадачи хуже имеющегося целочисленного решения, то эту подзадачу далее рассматривать не следует. В этом случае говорят, что задача прозондирована и ее следует вычеркнуть из списка подзадач. Таким образом, значение целевой функции для найденного целочисленного решения используется в качестве границы, которая позволяет сузить круг подзадач. Процесс ветвления продолжается до тех пор, пока каждая задача не приведет к целочисленному решению или не будет прозондирована. При этом зафиксированное наилучшее решение и будет оптимальным решением целочисленной задачи.
|

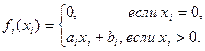
 , которую следует минимизировать. Функции
, которую следует минимизировать. Функции  (а, значит, и f (x)) не являются линейными из-за разрыва в начале координат. Введение дополнительных переменных позволяет свести эту задачу к линейной.
(а, значит, и f (x)) не являются линейными из-за разрыва в начале координат. Введение дополнительных переменных позволяет свести эту задачу к линейной. (2.14)
(2.14) становится линейной, а условие (2.14) можно записать в виде линейного неравенства:
становится линейной, а условие (2.14) можно записать в виде линейного неравенства: 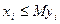 , где М достаточно велико для всех допустимых объемов выпуска продукции. Если
, где М достаточно велико для всех допустимых объемов выпуска продукции. Если  , то
, то  . Если же
. Если же  , то
, то  может быть равно как 0, так и 1. Но так как
может быть равно как 0, так и 1. Но так как  и ищется минимум целевой функции, то
и ищется минимум целевой функции, то  .
.


 ), (состоящую из нулей и единиц и называемую матрицей назначений), которая минимизирует целевую функцию
), (состоящую из нулей и единиц и называемую матрицей назначений), которая минимизирует целевую функцию

 или 1 (булевы переменные) при всех
или 1 (булевы переменные) при всех  .
. .Требуется найти самый короткий маршрут.
.Требуется найти самый короткий маршрут. – дробное число. Тогда, если все
– дробное число. Тогда, если все  (j = 1, 2, …, p) – целые, то задача не имеет целочисленных решений. Если среди
(j = 1, 2, …, p) – целые, то задача не имеет целочисленных решений. Если среди  ,
, 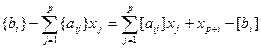 . (2.17)
. (2.17) > 0. С учетом целочисленности (правая часть уравнения (2.17) – целая) отсюда следует, что
> 0. С учетом целочисленности (правая часть уравнения (2.17) – целая) отсюда следует, что . (2.18)
. (2.18) и получаем {
и получаем {  }
}  0, а по предположению {
0, а по предположению { 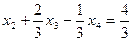 .
. ,
, , т. е.
, т. е.  .
. в оптимальном решении ослабленной задачи является дробным, то исходная задача разветвляется (разбивается) на две подзадачи. Каждая из них получается из ослабленной задачи добавлением соответственно неравенства
в оптимальном решении ослабленной задачи является дробным, то исходная задача разветвляется (разбивается) на две подзадачи. Каждая из них получается из ослабленной задачи добавлением соответственно неравенства  или
или 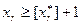 .
.


