Постановка задачи. Рассмотрим несколько примеров задач линейного программирования (ЗЛП)
Рассмотрим несколько примеров задач линейного программирования (ЗЛП). Задача о пищевом рационе (задача о диете, задача о смесях). Ферма производит откорм скота с коммерческой целью. Пусть имеются четыре вида продуктов: Р 1, Р 2, Р 3, Р 4 со стоимостью с 1, с 2, с 3, с 4 соответственно. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков – не менее b 1 единиц, углеводов – не менее b 2 единиц, жиров – не менее b 3 единиц. Для продуктов Р 1, Р 2, Р 3, Р 4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано таблицей.
Требуется составить такой пищевой рацион, чтобы условия по белкам, углеводам и жирам были выполнены и стоимость была минимальна. Составим математическую модель этой задачи. Пусть x 1, x 2, x 3, x 4 – количества продуктов Р 1, Р 2, Р 3, Р 4 соответственно, входящих в рацион. Целевая функция (стоимость рациона) будет иметь вид:
Ограничительные условия по белкам, углеводам и жирам приводят к следующим неравенствам:
Таким образом, задача сводится к следующей: найти такие неотрицательные значения переменных x 1, x 2, x 3, x 4, чтобы они удовлетворяли неравенствам (2.1) и обращали в минимум целевую функцию:
Задача об использовании сырья (задача планирования производства). Из сырья двух видов 1 и 2, запасы которого ограничены и составляют b 1 и b 2 единиц соответственно, изготавливается продукция трех видов. Затраты сырья на производство продукции задаются следующей таблицей.
Прибыль от производства единицы продукции j -го вида составляет cj рублей Обозначим x 1, x 2, x 3 соответственно количество производимой продукции 1-го, 2-го и
Задача об использовании мощностей (задача о загрузке оборудования). Ткацкая фабрика располагает двумя видами станков: N 1 станков типа 1 и N 2 станков типа 2. Станки могут производить три вида тканей: Т 1, Т 2, Т 3, но с разной производительностью. Станок типа i производит в месяц aij метров ткани вида Tj. Каждый метр ткани вида Tj приносит прибыль с j (j = 1, 2, 3). Согласно плану, фабрика должна производить в месяц не менее bj метров ткани Tj . Кроме того, все станки должны быть загружены. Требуется так распределить загрузку станков, чтобы суммарная месячная прибыль была максимальной. Пусть xij – количество станков типа i (i = 1, 2), занятых производством ткани
Целевой функцией, очевидно, является получаемая прибыль, т. е. Как видно из рассмотренных примеров, все эти задачи сходны между собой. Отличие состоит лишь в том, что в одних задачах требуется обратить линейную функцию в максимум, а в других в минимум; в одних ограничения – только неравенства, а в других – равенства и неравенства. Бывают задачи, где все ограничения – равенства. Эти различия несущественны, т. к., как будет показано позднее, от ограничений-неравенств легко переходить к равенствам и обратно. Общая задача линейного программирования состоит в нахождении экстремума (максимума или минимума) линейной целевой функции
при ограничениях
где aij, bi, cj ( Определение 2.1. Вектор Общая ЗЛП может быть приведена к единому стандартному виду, в котором целевая функция должна быть максимизирована, а все ограничения должны быть записаны в виде равенств с неотрицательными переменными:
при ограничениях
где Эта стандартная форма называется основной задачей линейного программирования (ОЗЛП). Запишем ее в матричном виде
при ограничениях Ax = b, x ≥ 0. Здесь
T означает транспонирование, т. е. сT – вектор-строка, Привести общую ЗЛП к основной очень просто, используя следующие очевидные правила. 1. Минимизация целевой функции f равносильна максимизации функции g = –f. 2. Ограничение в виде неравенства 3. Если на некоторую переменную xj не накладывается условие неотрицательности, то делают замену переменной
|

 .
. (2.1)
(2.1)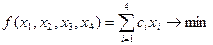 .
.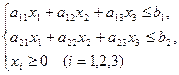
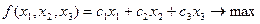



 (2.2)
(2.2)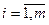 ,
, 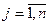 ) – заданные постоянные величины. Среди ограничений могут одновременно встречаться знаки ≤, =, ≥.
) – заданные постоянные величины. Среди ограничений могут одновременно встречаться знаки ≤, =, ≥. , удовлетворяющий системе ограничений (2.2), называется допустимым решением или планом ЗЛП. Множество всех планов называется допустимой областью или областью допустимых решений. План, который доставляет максимум (минимум), целевой функции называется оптимальным планом или оптимальным решением ЗЛП. Таким образом, решить ЗЛП – значит найти ее оптимальный план.
, удовлетворяющий системе ограничений (2.2), называется допустимым решением или планом ЗЛП. Множество всех планов называется допустимой областью или областью допустимых решений. План, который доставляет максимум (минимум), целевой функции называется оптимальным планом или оптимальным решением ЗЛП. Таким образом, решить ЗЛП – значит найти ее оптимальный план.

 ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, . A, b, c предполагаются известными, причем b ≥ 0.
. A, b, c предполагаются известными, причем b ≥ 0. равносильно уравнению
равносильно уравнению  при условии, что дополнительная переменная
при условии, что дополнительная переменная  . Аналогично,
. Аналогично, 

 ,
,  ,
,  .
.


