Геометрических тел

 

Цель работы: освоение методики изображения объемно-пространственной конструкции простых геометрических тел с помощью точек и линий на плоскости.

 

Основные положения:

При рисовании один предмет на листе, следует располагать его выше геометрического центра листа, получаемого пересечением диагоналей. Слева и справа необходимо оставить пространство, чтобы предмет не упирался в края бумаги или не был сдвинут в какую-то одну сторону (рис. 3.1)

Рис.. 3.1 Расположение рисунка на листе бумаги

Весь ход работы идет от общего к частному. Все предметы имеют объемно-пространст-венные характеристики: высоту, длину и ширину. Для определения и изображения их на плоскости пользуются точками и линиями.

Точками определяются характерные узлы конструкции предметов, ими устанавливается взаимное пространственное расположение узлов, характеризующее конструкцию формы в целом.

Линиями обозначают контуры предметов, образующие их форму. Ими обозначают высоту, длину, ширину, конструктивные оси, вспомогательные, определяющие пространства линии, линии построения.

Рис. 3.2 Определение пропорций предмета с помощью визирования

Перспективный рисунок геометрических тел может быть построен и проверен с помощью определенных приемов – это сравнение и визирование. Для определения основных размеров предмета в рисунке важны видимые, перспективно измененные их соотношения, а не реальные размеры объекта и его частей.

Для того чтобы выяснить сколько раз ширина постановки в натуре уложится в ее высоте, т.е., пропорции габаритных размеров надо применить методику визирования (рис. 3.2).

Берется произвольный измеритель (чаще всего это карандаш) таким образом, чтобы он был свободным концом визуально совмещен с одним краем измеряемого предмета, а другой край этого предмета отмечают большим пальцем. При этом обязательно необходимо соблюдать два условия:

1. Расстояние от глаза до измерителя должно быть всегда одинаково. Для этого измеритель надо держать всегда на вытянутой руке.

2. Измеритель должен быть всегда перпендикулярен лучу зрения.

Рис.. 3.3 Определение габаритных размеров предмета с помощью визирования

3. Необходимо совместить концы измерителя с горизонтальными габаритами постановки. Полученный размер укладываем в вертикальном габаритном размере постановки (всегда меньшее укладываем в большем). Сначала один раз от крайней нижней точки вверх, затем, мысленно отметив уровень верхнего конца измерителя, вверх от этого уровня.

В данном случае измеритель уложится немного больше, чем один раз с половиной. Это и есть пропорция: примерно 1/1. Теперь на рисунке уже отмеченную ранее ширину укладывают в высоте. Таким образом получены габариты постановки. (рис. 3.3)

Надо обратить особое внимание, что с натуры надо брать не линейный размер, а именно пропорцию. Линейные размеры в рисунке и в постановке совпадать не будут и не должны. Все оставшиеся размеры строятся в пропорции к уже имеющимся.

Существует еще одна методика визирования

Рис. 3.4 Определение угла наклона линий с помощью визирования

– визирование по направлениям для выяснения угла наклона линий. При этом: визуально совмещают измеритель, держа его на вытянутой руке, с измеряемой линией в натуре.

Затем, не сгибая руку в локте, переносят измеритель и совмещают его с плоскостью рисунка, проводят линию под таким же углом наклона. (рис 3.4)

 

 

Важным моментом для развития объемно-пространственного мышления является понимание конструкции предмета. Конструкция – обобщенное понимание формы, сведение ее к простым и легким для представления геометрическим объемам. Использование при обучении рисунку каркасных моделей для рисования с натуры позволяет лучше освоить конструктивную сущность предмета и пространственность его формы.

Любая форма состоит из плоских фигур, которые отграничивают ее от окружающего пространства. Плоские геометрические фигуры служат основой понимания конструктивного построения объемных тел. Так, например, квадрат дает представление о построении куба, прямоугольник — о построении призмы параллелепипеда, треугольник — пирамиды, круг представляется шаром, цилиндром и конусом (рис. 3.5).

Основополагающим принципом в освоении рисунка простых геометрических форм является умение правильно отображать объемно-пространственную конструкцию форм с помощью точек и линий на плоскости. Соблюдая принцип «от простого к сложному», необходимо вначале изучить простые геометрические тела: куб, призму, пирамиду (рис. 3.6).

		Рис. 3.5 Плоские геометрические фигуры служат основой конструктивного построения объемных тел.
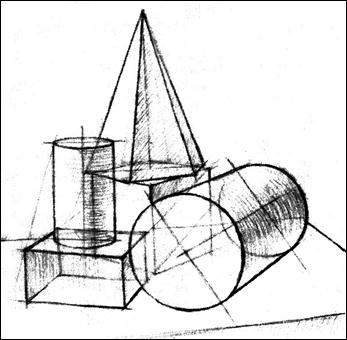
	Рис. 3.6 Конструктивный рисунок натюрморта из объемных тел.

 

 

Рисование куба

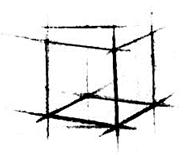
Куб является одним из самых простых геометрических тел. Чтобы лучше понять геометрическую форму куба, его пространственную конструктивную схему (структуру), рассмотрим каркас куба. Это дает возможность ясно представить объемно-пространственную характеристику его формы, позволяет видеть его конструктивные узлы — точки, невидимые на обычных телах.

Соотношения сторон куба составляют пропорцию 1: 1: 1. Для того чтобы куб выглядел достоверно в трехмерном изображении, следует определить такую точку зрения, при кото- рой предмет выглядит достаточно убедительным в объеме. Изображение каркаса куба производится с учетом его пропорций, по законам перспективы. Рисование куба выполняется в следующей последовательности (рис. 3.7):

1. Выполняется компоновка листа, нахождение размера рисунка по отношению к листу. Изображение не должно быть больше натуральной величины. Расстояние по бокам изображения должно быть примерно равным. Сверху расстояние больше, чем снизу.

2. Находится линия горизонта.

Рис. 3.7 Последовательность рисования каркасной модели куба.

3. Выполняется линейная разработка общих пропорций. Изображение намечается легки- ми линиями с боков, сверху и снизу. С учетом ракурса, пропорций и перспективы определяются основные конструктивные точки вершин углов куба. Находится точка, ближе всего расположенная к лучу зрения.

4. С учетом перспективных сокращений по конструктивным точкам вершин углов намечается общая форма конструкции куба.

5. Проводится построение вертикальных линий ребра куба.

6. Находится угол наклона боковых ребер по отношению к линии параллельной низу листа, длины отрезков в перспективе.

7. Определяется второй угол основания куба.

 

8. Строится основание куба – квадрата в перспективе.

9. Проводится построение вертикальных ребер куба в перспективе.

10. Определяются длины четырех сторон куба и строят верхнюю плоскость куба. Линии по мере удаления должны ослабевать для создания пространственной глубины.

Рис. 3.8 Рисунок каркасного куба

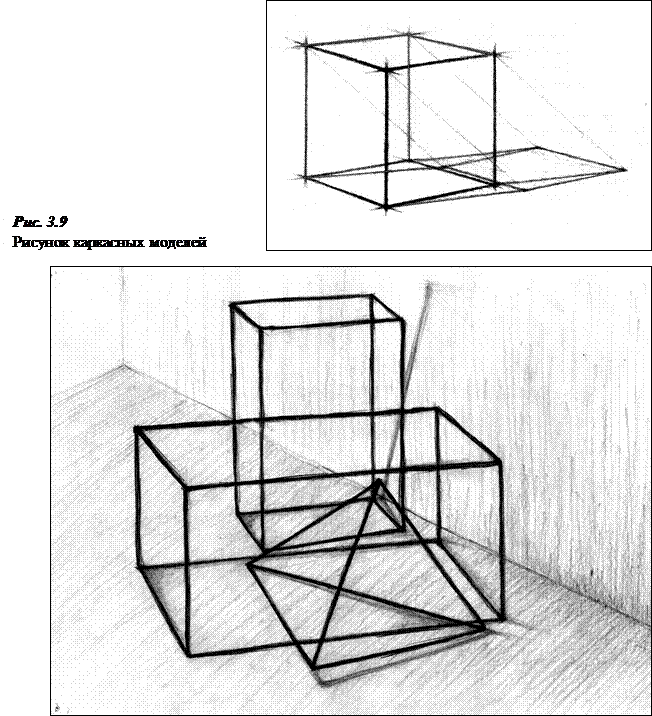
На рис. 3.9 показаны рисунки каркасных моделей

 

 

Рисование призмы

Шестигранная призма характеризуется шестиугольником в основании и шестью линиями ребер. Ее ось определяется линиями, проведенными от противоположных простран­ственных углов основания, где точка их пересечения будет центром, через который проходит ось призмы.

Для правильного определения еепространственных углов, необходимо начинать работу с построения эллипса и окружности под ним. В соответствии с видимым положением предмета при данной точке зрения следует правильно определить на окружности точки пространственных углов правильного шестигранника.

Рис. 3.10 Последовательность рисования шестигранной призмы

Сложность состоит в правильном определении с видимого положения перспективно сокращенных граней, их пропорциональных отношений. В этом случае следует пользоваться вспомогательной окружностью в плане у нижнего основания призмы (рис.3.10).

На окружности основания призмы важно правильно отложить равные отрезки и определить шесть пространственных углов по окружности с учетомповорота призмы, т.е. с видимого положения. Соединяя точки линиями, необходимо проследить за параллельностью противоположных сторон.

Получив точки пространственных углов основания призмы, следует перенести их на нижнее основание эллипса. При переносе пространственных углов на основание эллипса учитывают перспективное сокращение его дальней половины.

Для определения верхнего основания призмы следует повторить рисунок эллипса, после чего, соединяя вертикальными линиями ребер пространственные точки оснований, получают построение изображения шестигранной призмы. На перспективном изображении призмы окружность (эллипс) нижнего основания должна быть несколько шире верхней.

Трехгранная пирамида (рис. 3.11) характеризуется треугольником в основании, точкой вершины и шестью линиями ребер. Для правильного изображения пирамиды рисунок следует начинать с построения ее основания, что аналогично построению призматической формы. Соединив точки пространственных углов основания линиями, надо найти конструктивную ось пирамиды и точку ее вершины.

Положение конструктивной оси определяется линиями, проведенными из углов основания перпендикулярно к его сторонам. От точкипересечения проводят вертикальную линию.

Рис. 3.11 Последовательность рисования трехгранной пирамиды

Затем необходимо определить положение точки вершины пирамиды на осевой линии, в соответствии с высотой пирамиды. После чего следует соединить вершину с пространственными углами основания.

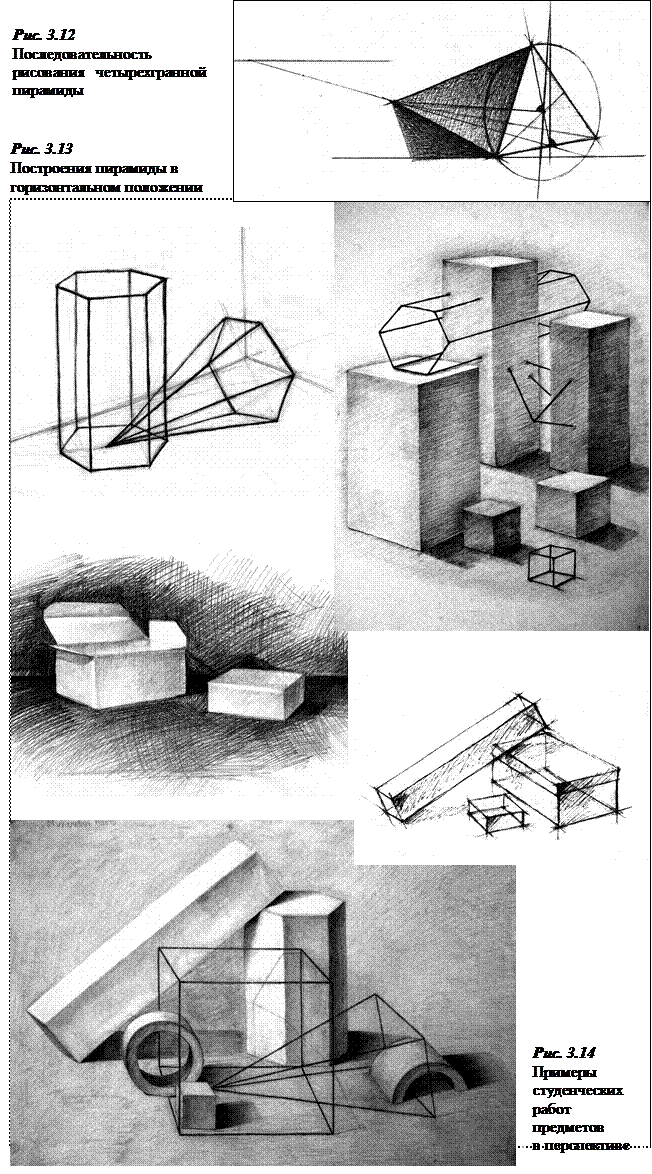
Четырехгранная пирамида строится аналогично трехгранной (рис. 3.13).

При построении пирамиды в горизонтальном положении следует обратить внимание на положение оси пирамиды по отношению к центру ее основания. При этом плоскость основания пирамиды по отношению к ее конструктивной оси должна находиться строго под прямым углом, то есть перпендикулярно, независимо от положения предмета при данной точке зрения. Структура строения тела также остается неизменной.

 

Задание:

Выполнить рисунки отдельных геометрических тел с соблюдением законов линейной перспективы и пропорций.