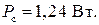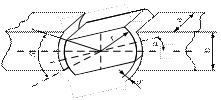
Примеры решения задач. 5.1. Определить суммарную магнитную проводимость рабочих зазоров между якорем и полюсами электромагнитного механизма5.1. Определить суммарную магнитную проводимость рабочих зазоров между якорем и полюсами электромагнитного механизма, представленного на рисунке 5.1. Размеры полюсов:
Рис. 5.1. Полюса электромагнитного механизма Решение. Для концентрических полюсов с постоянными значениями зазора, толщины, ширины и радиуса, проводимость без учета потока выпучивания определяется по формуле (табл. П.14)
где Ответ:
5.2. Определить суммарную магнитную проводимость рабочих зазоров и удельную проводимость рассеяния прямоходового электромагнита (рис. 5.2). Геометрические размеры электромагнита:
Рис. 5.2 Полюса прямоходового электромагнита с внешним якорем Решение. Магнитная проводимость одного рабочего зазора определяется по формуле (табл. П.14)
где Суммарная проводимость
Удельная проводимость рассеяния (табл. П.14)
где Ответ: 5.3. Определить величину тока возбуждения для создания индукции в тороиде Внутренний диаметр тороида Решение. Активное сечение магнитопровода
Величина магнитного потока
По индукции из кривых (рис. П.7) находим Тогда магнитные сопротивления тороида
Величина и фаза тока
Потери на вихревые токи и гистерезис в стали
где Ответ:
|
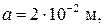
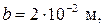
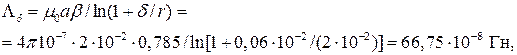
– угол сдвига между осью полюсов и осью якоря; 
– угол перекрытия.
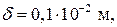
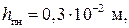
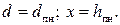
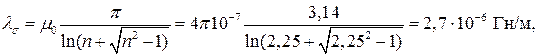
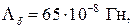
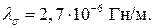
и найти потери в стали.
радиальная ширина 
толщина пакета тороида 
марка стали – 1511, толщина листов 
коэффициент заполнения стали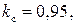 
число витков обмотки 
частота переменного тока 
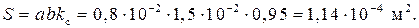
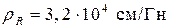и 
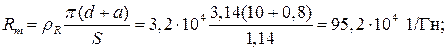
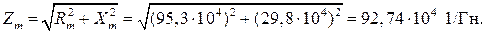
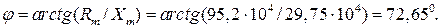
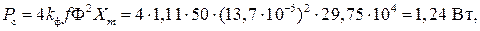
– коэффициент формы поля.
