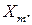Краткие теоретические сведения. Магнитные цепи находят широкое применение в различных электрических аппаратах (электромагнитных устройствах
Магнитные цепи находят широкое применение в различных электрических аппаратах (электромагнитных устройствах, контакторах, автоматах, приводах выключателей, тормозных, тяговых, подъемных электромагнитах, реле, датчиках, электромагнитных муфтах, дросселях и других). Под магнитной цепью понимается совокупность тел и сред, создающая ориентированный магнитный поток при наличии магнитодвижущей силы. Магнитные цепи можно разбить на два основных вида: цепи с малым потоком рассеяния и цепи с большим потоком рассеяния. С достаточной для практики точностью потоком рассеяния можно пренебречь в тех случаях, когда он мал по сравнению с основным потоком: 1) магнитопровод замкнут; 2) на пути основного потока имеется воздушный зазор сравнительно малой величины, а магнитная цепь насыщена незначительно; 3) размагничивающее действие вторичной обмотки сравнительно невелико. Методы расчета магнитных цепей основываются на законах Ома и Кирхгофа применительно к магнитным цепям. При этом используются аналитические и графоаналитические методы. Основные трудности расчета магнитных цепей связаны с учетом нелинейной магнитной характеристики, потерь в стали и размагничивающего действия магнитных экранов. При расчете магнитной цепи определяется МДС обмотки, необходимая для создания заданного рабочего потока (прямая задача), или рабочий поток по известной МДС (обратная задача). Эти задачи решаются с помощью уравнений Кирхгофа для магнитной цепи. Согласно первому закону Кирхгофа алгебраическая сумма потоков в любом узле магнитной цепи равна нулю
Второй закон Кирхгофа следует из известного закона полного тока. Падение магнитного потенциала по замкнутому контуру равно сумме МДС, действующих в этом контуре
где Расчет магнитных цепей подобен расчету электрических цепей и основан на применении уравнений (5.1) – (5.2). Так как индукция
где Выражение
где Когда поток в отдельных участках магнитной цепи не меняется интеграл в (5.4) можно заменить суммой
Направление МДС, совпадающее с направлением обхода контура, принимается за положительное. Из (5.5) вытекает закон Ома для магнитной цепи, при этом вместо тока подставляется магнитный поток, вместо электрического сопротивления – магнитное, вместо электродвижущей силы – магнитодвижущая (МДС). По аналогии с электрическим сопротивлением магнитное можно представить как
где Для расчета по (5.5) необходимо знать
По известной индукции в каждом участке с помощью кривой намагничивания находят напряженность При расчете магнитной цепи часто более удобной является величина, обратная магнитному сопротивлению, – магнитная проводимость, Гн
Уравнение (5.5) при этом принимает вид
Магнитное сопротивление и проводимость ферромагнитных материалов являются сложной нелинейной функцией индукции, что затрудняет решение как прямой, так и обратной задачи. Магнитная проницаемость воздушного зазора является постоянной величиной. Для сравнительно простых форм полюсов проводимости воздушных зазоров могут быть вычислены аналитически. Например, для полюсов при малом воздушном зазоре
Для сравнительно больших зазоров необходимо учитывать выпучивание. Расчет в этом случае для полюсов простых форм проводят по эмпирическим формулам (табл. П.14). Для полюсов более сложных форм аналитические выражения отсутствуют, и проводимости могут быть рассчитаны графическими методами (построение картины поля), методом вероятных путей потока (разбивки области поля на простейшие геометрические фигуры, для которых известны аналитические выражения). При переменном напряжении ток в обмотке определяется в основном ее индуктивным сопротивлением, которое меняется при перемещении якоря. Магнитное сопротивление магнитопровода на переменном токе зависит не только от Расчет магнитной цепи переменного тока ведется с помощью законов Кирхгофа в комплексной форме методом последовательных приближений. При расчете принимается синусоидальное изменение напряжения, тока и потока. Если же магнитная цепь работает при сравнительно больших индукциях (за коленом кривой намагничивания), то расчет ведется по первой гармонике.
|

 (5.1)
(5.1) (5.2)
(5.2) – напряженность магнитного поля;
– напряженность магнитного поля;  – элементарный участок контура интегрирования;
– элементарный участок контура интегрирования; 
 – алгебраическая сумма МДС, действующих в контуре,
– алгебраическая сумма МДС, действующих в контуре,  – число витков обмотки.
– число витков обмотки. (
(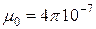 Гн/м – магнитная проницаемость воздуха;
Гн/м – магнитная проницаемость воздуха; 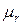 – относительная магнитная проницаемость) можно записать
– относительная магнитная проницаемость) можно записать (5.3)
(5.3) – сечение данного участка магнитной цепи.
– сечение данного участка магнитной цепи. аналогично выражению для активного сопротивления элемента электрической цепи. Выражение (5.3) можно представить в виде
аналогично выражению для активного сопротивления элемента электрической цепи. Выражение (5.3) можно представить в виде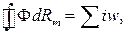 (5.4)
(5.4) – магнитное сопротивление участка длиной
– магнитное сопротивление участка длиной  (5.5)
(5.5)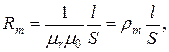 (5.6)
(5.6) – магнитное сопротивление единицы длины магнитной цепи при сечении, равном единице, м/Гн.
– магнитное сопротивление единицы длины магнитной цепи при сечении, равном единице, м/Гн. , а кривая намагничивания материала
, а кривая намагничивания материала  , для расчета удобно использовать выражение (5.2). Если на отдельных участках магнитной цепи индукция постоянна, то интеграл в (5.2) можно заменить суммой
, для расчета удобно использовать выражение (5.2). Если на отдельных участках магнитной цепи индукция постоянна, то интеграл в (5.2) можно заменить суммой (5.7)
(5.7) , после чего с помощью (5.7) можно отыскать МДС обмотки.
, после чего с помощью (5.7) можно отыскать МДС обмотки. (5.8)
(5.8) (5.9)
(5.9) между ними поле можно считать равномерным, а проводимость определить по формуле
между ними поле можно считать равномерным, а проводимость определить по формуле (5.10)
(5.10) , но и от потерь в стали и наличия короткозамкнутых витков. Потери в стали в схеме замещения магнитной цепи переменного тока учитываются с помощью реактивного магнитного сопротивления
, но и от потерь в стали и наличия короткозамкнутых витков. Потери в стали в схеме замещения магнитной цепи переменного тока учитываются с помощью реактивного магнитного сопротивления