Статистической оценкой параметра называется его приближенное значение, полученное на основе выборочных данных. Для получения точечных оценок параметров уравнения парной линейной регрессии применяют метод наименьших квадратов (МНК). В соответствии сМНК минимизируется сумма квадратов разностей между фактическими и расчетными значениями зависимой переменной. Оценки неизвестных параметров находятся из системы нормальных уравнений, полученной методом дифференциального исчисления.
Для расчета интервальных оценок (доверительных интервалов) параметров регрессии определяются предельные ошибки  для каждого показателя: для каждого показателя:  , где , где 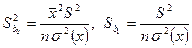 – стандартные ошибки коэффициентов регрессии, – стандартные ошибки коэффициентов регрессии, 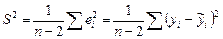 – стандартная ошибка регрессии, которая служит мерой разброса зависимой переменной вокруг линии регрессии, – стандартная ошибка регрессии, которая служит мерой разброса зависимой переменной вокруг линии регрессии,  – критическая точка распределения Стьюдента для заданного уровня значимости – критическая точка распределения Стьюдента для заданного уровня значимости 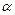 и числа степеней свободы и числа степеней свободы 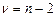 . Доверительные интервалы имеют вид: для . Доверительные интервалы имеют вид: для  ( (  ), для ), для  ( (  ).
Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения. ).
Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
|
В результате проведения регрессионного анализа на листе Регрессия в третьей таблице получены точечные и интервальные оценки неизвестных параметров.
Таблица 1.6 – Статистика коэффициентов регрессии
|
| Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| Нижние 95%
| Верхние 95%
|
| Y-пересечение
| -73, 25
| 16, 03
| -4, 57
| 0, 000238
| -106, 93
| -39, 56
|
| ВВП
| 0, 26
| 0, 01
| 25, 93
| 0, 000000
| 0, 24
| 0, 28
|
|
|
| tкр
| 2, 1009
|
|
|
|
Точечная оценка параметра 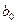 равна -73, 25. Интервальная оценка равна (-106, 93; -39, 56), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t-статистики. Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра
равна -73, 25. Интервальная оценка равна (-106, 93; -39, 56), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t-статистики. Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра 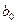 .
.
Точечная оценка параметра 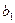 равна 0, 24. Интервальная оценка равна (0, 24; 0, 28). Доверительный интервал с вероятностью 0, 95 содержит истинное значение коэффициента при переменной x уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра
равна 0, 24. Интервальная оценка равна (0, 24; 0, 28). Доверительный интервал с вероятностью 0, 95 содержит истинное значение коэффициента при переменной x уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра  .
.
Таким образом, уравнение регрессии имеет вид
y = -73, 25 + 0, 24 x.
Случайная переменная отсутствует в уравнении, так как коэффициенты регрессии имеют случайный характер, т. е. неучтенные факторы повлияли на их значение при применении МНК.

 для каждого показателя:
для каждого показателя:  , где
, где 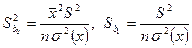 – стандартные ошибки коэффициентов регрессии,
– стандартные ошибки коэффициентов регрессии, 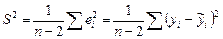 – стандартная ошибка регрессии, которая служит мерой разброса зависимой переменной вокруг линии регрессии,
– стандартная ошибка регрессии, которая служит мерой разброса зависимой переменной вокруг линии регрессии,  – критическая точка распределения Стьюдента для заданного уровня значимости
– критическая точка распределения Стьюдента для заданного уровня значимости 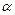 и числа степеней свободы
и числа степеней свободы 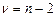 . Доверительные интервалы имеют вид: для
. Доверительные интервалы имеют вид: для  (
(
 ), для
), для  (
(
 ).
Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
).
Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
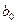 равна -73, 25. Интервальная оценка равна (-106, 93; -39, 56), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t-статистики. Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра
равна -73, 25. Интервальная оценка равна (-106, 93; -39, 56), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t-статистики. Доверительный интервал с вероятностью 0, 95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра 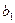 равна 0, 24. Интервальная оценка равна (0, 24; 0, 28). Доверительный интервал с вероятностью 0, 95 содержит истинное значение коэффициента при переменной x уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра
равна 0, 24. Интервальная оценка равна (0, 24; 0, 28). Доверительный интервал с вероятностью 0, 95 содержит истинное значение коэффициента при переменной x уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра  .
.


