Для студентов экономических специальностей
БЕЛОРУССКИЙ РЕСПУБЛИКАНСКИЙ СОЮЗ
Часть 3
Гомель 2011 УДК … ББК … …. Авторы-составители: Л. П. Авдашкова, канд. физ.-мат. наук, доцент, Рецензенты: Л. В. Федосенко, канд. экон. наук, доцент кафедры финансов и кредита ГГУ им. Ф. Скорины; Рекомендован кафедрой информационно-вычислительных систем учреждения образования «Белорусский торгово-экономический университет потребительской кооперации». Протокол № 10 от 18 мая 2011 г. Рекомендован к изданию научно-методическим советом УО «Белорусский торгово-экономический университет потребительской кооперации». Протокол № от мая 2011 г.
УДК … ББК … В практикуме излагаются технология построения и анализ эконометрических моделей с использованием MS Excel. Практикум предназначен для использования при аудиторной и самостоятельной работе студентов экономических специальностей и всех, интересующихся эконометрикой.
СОДЕРЖАНИЕ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.. 4 ВВЕДЕНИЕ.. 5 ТЕМА 1. ПАРНАЯ РЕГРЕССИЯ.. 9 Постановка задачи. 9 Технология вычислений в Excel для построения и анализа линейной парной регрессии 9 Анализ эконометрической модели парной регрессии. 18 Вопросы для самоконтроля. 38 Индивидуальные задания. 40 ТЕМА 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ.. 41 Постановка задачи. 41 Технология вычислений в Excel для построения и анализа линейной множественной регрессии 42 Анализ эконометрической модели множественной линейной регрессии. 51 Вопросы для самоконтроля. 63 Индивидуальные задания. 65 ТЕМА 3. ВРЕМЕННЫЕ РЯДЫ... 66 Постановка задачи. 66 Технология вычислений в Excel при построении модели временного ряда. 66 Анализ модели временного ряда. 69 Вопросы для самоконтроля. 79 Индивидуальные задания. 79 ТЕМА 4. ЗАВИСИМОСТЬ ПЕРЕМЕННЫХ, ЗАДАННЫХ ВРЕМЕННЫМИ РЯДАМИ 79 Постановка задачи. 79 Технология вычислений в Excel взаимосвязи двух временных рядов. 80 Анализ модели. 84 Вопросы для самоконтроля. 93 ТЕМА 5. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ.. 93 Постановка задачи. 93 Технология выполнения работы.. 94 Анализ модели. 96 Вопросы для самопроверки. 101 Индивидуальные задания. 102 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 103
Пособие предназначено для студентов экономических специальностей для организации аудиторной и самостоятельной работы. Эконометрическое моделирование предполагает получение модели и ее анализ на качество по определенным статистическим параметрам, которые необходимо найти, используя знания математической статистики. Поэтому вначале предлагается выполнить вычисления параметров с помощью приложения MS Excel, описанные в разделе «Технология вычислений в MS Excel …», а затем провести дальнейший анализ построения и оценки модели с помощью полученных значений параметров. Такой подход при построении занятия позволяет, с одной стороны, вспомнить сведения из математической статистики и применить их для решения конкретной задачи эконометрического моделирования на этапе расчетов, с другой стороны, на этапе анализа акцентировать внимание на необходимость выполнения определенных статистических условий, не отвлекаясь на выполнение вычислений. По каждой теме в пособии предлагается технология вычислений, анализ по полученным параметрам соответствующей модели, вопросы для самоконтроля, индивидуальные задания. Так как этапы эконометрического моделирования справедливы для любой модели, то в пособии в разделах по технологии вычислений и анализа модели используется одинаковая нумерация этих этапов. В разделе «Анализ модели …» для каждого этапа эконометрического моделирования приводится соответствующий теоретический материал, который позволяет организовать обсуждение проблемных ситуаций, улучшить организацию самостоятельной работы, ответить на вопросы для самоконтроля. Индивидуальные задания позволяют организовать самостоятельную работу студентов. Нумерация рисунков, таблиц осуществляется в каждой теме отдельно.
ВВЕДЕНИЕ Постоянно усложняющиеся экономические процессы требуют повышения уровня образования современных специалистов по экономике и управлению. Изучение дисциплины «Эконометрика и экономико-математические методы и модели» позволяет использовать моделирование и количественный анализ в экономических исследованиях. Специалист экономического профиля для решения поставленных задач должен владеть научными основами исследования социально-экономических систем, анализа исходных данных, формализации, прогнозирования и принятия оптимальных управленческих решений, используя для этой цели современные технические средства. Экономические исследования требуют от экономистов умений применять экономико-математические методы, создавать эконометрические модели, основываясь на знании экономической теории, экономической статистики, математического моделирования, теории вероятностей, математической статистики и математическое моделирования для понимания количественных взаимосвязей между экономическими факторами в целях анализа и прогнозирования реальных экономических процессов. Данный практикум предназначен для студентов экономических специальностей, подготовлен в соответствии с программой курса «Эконометрика и экономико-математические методы и модели». Структура и содержание практикума, его терминология базируются на программе курса и отвечают современным достижениям в данной отрасли науки. Он качественно дополняет учебно-методический арсенал университета, обеспечивая методическую и компьютерную поддержку опыта построения стохастических моделей на основе пространственных и временных данных хозяйственной деятельности реальных экономических объектов и процессов. В практикуме рассмотрены основные эконометрические вопросы, связанные с: · построением классических линейных регрессионных моделей (парных и множественных); · изучением эконометрических моделей, выраженных системой одновременных уравнений; · анализом структуры временных рядов и изучением взаимосвязей между ними; · рассмотрением основных ошибок, возникающих при нарушении классических модельных предположений, методикой их диагностики и устранения. При изложении учебного материала предполагается, что читатель владеет знаниями по экономической теории, основам теории вероятностей и математической статистики, экономической статистики в объеме соответствующего курса для экономических специальностей. Экономическая теория с помощью качественного анализа устанавливает совокупность факторов и показателей, влияющих на изучаемое экономическое явление, их роль и теоретические взаимосвязи. Экономическая статистика обеспечивает информационную базу экономических исследований, обеспечивая первичную обработку эмпирических значений выбранных экономических показателей. Экономическая статистика, как правило, ограничивается простейшими качественными выводами. Математическая статистика обеспечивает инструментом работы со случайными величинами. Математическое моделирование формализует рассматриваемую экономическую задачу на языке математики. Эконометрика оценивает количественные взаимосвязи изучаемых факторов и использует эти оценки для прогнозирования экономических процессов. Одной из основных задач эконометрики является построение и анализ эконометрической модели. При этом под эконометрической моделью понимается такая форма представления исследуемой экономической задачи с помощью математических терминов и соотношений на основе статистических данных, которая удобна для проведения количественного анализа. Существуют различные классификации эконометрических моделей. Например, одна из них выделяет типы эконометрических моделей по фактору времени: различают статические и динамические (модели временных рядов) эконометрические модели. Первые из них исследуют состояние системы в определенный момент времени (то есть опираются на единовременный срез информации по изучаемым объектам). Вторые строятся по данным, характеризующим изучаемые объекты за ряд последовательных периодов времени, то есть они используют не только текущие значения показателей, но и некоторые предыдущие по времени значения, а также и само время t. В зависимости от формы математического представления эконометрические модели подразделяют на модели с одним уравнением и модели системы одновременных уравнений. В первом случае объясняемый фактор y выражается через объясняющие переменные Модели системы одновременных уравнений используются при изучении достаточно сложных экономических явлений взаимосвязи между исследуемыми показателями, которые описываются не одним, а несколькими уравнениями. Например, модель равновесия спроса и предложения в рыночной экономике. Выделяют следующие этапы решения эконометрической задачи. 1. Постановочный этап предполагает определение целей и задач исследования; выделение факторов и показателей, определяющих изучаемые экономические процессы; установление на базе экономической теории роли выбранных показателей. 2. Этап спецификации предполагает выбор формулы связи между переменными, обозначающими выделенные факторы. Эта формула имеет общий вид и содержит параметры (коэффициенты при переменных), требующие статистической оценки. 3. Этап параметризации решает задачу оценки значений параметров выбранной функции связи. 4. Этап верификации предполагает проверку адекватности модели, то есть проверку соответствия модели реальному экономическому явлению или процессу. Кроме того, здесь выясняется, насколько удачно решены проблемы спецификации и параметризации, совершенствуется форма модели, уточняется состав объясняющих переменных, устанавливается точность расчетов по данной модели, общее качество уравнения, статистическая значимость найденных параметров, а также разрешаются многие другие вопросы, определяющие надежность выводов по модели. Реальное значение зависимой переменной y не совпадает с условным математическим ожиданием Таким образом, величина y разбивается на две части: одна из них (объясняемая) задает ту часть y, которая объясняется факторами Уравнение Общая задачи эконометрического моделирования заключается в следующем: по имеющимся данным n наблюдений за изменением признака y в зависимости от наборов значений факторов
ТЕМА 1. ПАРНАЯ РЕГРЕССИЯ Постановка задачи Исследовать зависимость объема экспорта (y, усл. ед.) от валового внутреннего продукта (ВВП) (x, усл. ед.), используя данные 20 наблюдений, приведенные в таблице 1.1. Построитьрегрессионную модель Таблица 1.1 – Исходные данные
Технология вычислений в Excel для построения и анализа линейной парной регрессии 1. Постановочный этап: определение целей и задач исследования; выделение факторов и показателей, определяющих изучаемые экономические процессы; установление роли выбранных показателей; подготовка данных для расчетов. Из экономической теории известно, что экспорт зависит от многих факторов, например, от ВВП, ценовой политики, сертификации и стандартизации продукции, политики других государств, таможенных пошлин и т. д. Выделим один фактор – ВВП, который является наиболее существенным. Он называется объясняющим фактором (x) для результативного (объясняемого) фактора (y) – экспорт. Поэтому возникает задача количественного описания зависимости указанных экономических показателей уравнением парной регрессии. Подготовьте данные для расчетов. В ячейку А1 введите название ВВП, в ячейку В1 — Экспорт. В ячейки А2, …, А21 введите значения ВВП, в ячейки В2, …, В21 — соответствующие значения экспорта. Переименуйте лист 1 в «Исходные данные», щелкнув правой клавишей мыши на ярлыке «Лист 1» и выбрав команду переименование или в режиме редактирования после двойного щелчка левой клавишей мыши на ярлыке «Лист 1». Сохраните открытый файл «Книга1» под названием «Фамилия-регрессия», например, в папке «Мои документы» (Файл – Сохранить как – Папка Мои документы – Имя файла – Фамилия-регрессия – Сохранить).
2. Спецификация: выбор в общем виде формулы связи между переменными, обозначающими выделенные факторы. Вид и сила функциональной зависимости (линейная или нелинейная) определяется по ковариации и коэффициенту корреляции. В меню Сервис выберите команду Анализ данных. Замечание.Если в меню отсутствует эта команда, то следует выбрать Сервис – Надстройка – установить флажок Пакет анализа. При необходимости перезагрузить компьютер. Выделите анализ Ковариация, нажмите кнопку ОК. Установите значения параметров в появившемся диалоговом окне следующим образом: · Входной интервал – введите ссылки на диапазон ячеек А1: В21 (курсор установите в поле Входной интервал, указатель мыши поместите в ячейку А1, удерживая нажатой левую клавишу, протяните указатель мыши до ячейки В21); · Группирование – флажок по столбцам устанавливается автоматически; · Метки в первой строке – установите флажок щелчком левой клавиши мыши; · Параметры вывода – установите флажок на Выходной интервал, поставьте курсор в поле напротив, выделите ячейку D2. Нажмите ОК. В ячейке D1 введите слово Ковариация – название таблицы. В меню Сервис выберите команду Анализ данных и выделите анализ Корреляция. Установите следующим образом значения параметров: · Входной интервал – введите ссылки на ячейки, содержащие исходные данные А1: В21 (курсор установите в поле Входной интервал, указатель мыши поместите в ячейку А1, удерживая нажатой левую клавишу, протяните указатель мыши до ячейки В21); · Группирование – флажок по столбцам устанавливается автоматически; · Метки в первой строке – установите флажок; · Параметры вывода – установите флажок на Выходной интервал, поставьте курсор в поле напротив, выделите ячейку D7. Нажмите ОК. В ячейке D6 введите слово Корреляция — название таблицы. Для проверки гипотезы о значимости коэффициента корреляции сравниваются наблюдаемое В ячейку D11 введите обозначение tнабл. В ячейку E11 введите формулу =Е9*КОРЕНЬ(20-2)/КОРЕНЬ(1-Е9^2) для вычисления tнабл, где 20 — число наблюдений, 2 — число факторов. В ячейку D12 введите tкр. В ячейке E12 вычислите критическое значение tкр следующим образом: – нажмите на fx (вставка функций); – в поле Категория окна Мастер функций выберите статистические, из предложенных ниже функций выделите СТЬЮДРАСПОБР и нажмите «ОК». Откроется окно Аргументы функции. Заполните поля: · Вероятность — наберите значение альфа, равное 0, 05; · Степени свободы — введите 20-2, где 20 — число наблюдений, 2 — число факторов (x, y). Нажмите ОК. Замечание 1. Выводы о существовании зависимости и выборе вида функции связи подробно описаны в разделе «Анализ эконометрической модели парной регрессии». Замечание 2. Предполагаем, что между ВВП (х) и экспортом (у) существует линейная зависимость. Далее находится уравнение парной линейной регрессии. Если доказана нелинейность зависимости, то проводится процедура линеаризации (см. [9]). 3. Параметризация модели: нахождение оценок значений параметров выбранной функции связи. Найдите МНК-оценки неизвестных параметров В меню Сервис выберите команду Анализ данных, укажите анализ Регрессия. Нажмите ОК. Установите в появившемся окне значения параметров следующим образом: · Входной интервал Y — введите ссылки на ячейки В1: В21; · Входной интервал X — введите ссылки на ячейки А1: А21; · Метки — установите флажок; · Уровень надежности — установите флажок; · Константа ноль — не активизируйте; · Параметры вывода — установите переключатель на Новый рабочий лист и в поле напротив введите слово Регрессия; · Остатки — установите флажок; · Стандартизированные остатки — оставьте пустым; · График остатков — установите флажок; · График подбора — установите флажок; · График нормальной вероятности — оставьте пустым. Нажмите ОК. Расположите диаграммы рядом (на поле диаграммы нажмите левую клавишу мыши, затем поместите курсор на белое поле и при нажатой левой клавише передвигайте диаграмму вниз) и растяните (на поле диаграммы нажмите левую клавишу мыши, нижнюю линию границы диаграммы при нажатой левой клавише протяните вниз). Замечание. Выводы о значениях оценок параметров уравнения регрессии подробно описаны в разделе «Анализ эконометрической модели парной регрессии». 4. Верификация модели: проверка адекватности модели. 4.1. Общее качество уравнения: проверка значимости коэффициента детерминации. Для проверки гипотезы о значимости коэффициента детерминации сравниваются наблюдаемое значение статистики Фишера, найденное с помощью анализа Регрессия, и критическое значение – нажмите на fx (вставка функций); – в поле Категория окна Мастер функций выберите статистические, из предложенных ниже функций выделите FРАСПОБР и нажмите ОК. Откроется окно Аргументы функции. Заполните поля так: · Вероятность — наберите значение 0, 05; · Степени свободы 1 — установите курсор в поле и выделите ячейку В12 столбца df таблицы «Дисперсионный анализ»; · Степени свободы 2 — установите курсор в поле и выделите ячейку В13 столбца df таблицы «Дисперсионный анализ». Нажмите ОК. В ячейку D15 введите обозначение – Fкр. Замечание. Выводы о качестве уравнения подробно описаны в разделе «Анализ эконометрической модели парной регрессии». 4.2. Нормальность распределения остатков: устанавливается для возможности использования статистики Стьюдента при проверке гипотез (визуально по гистограмме, по асимметрии и эксцессу, с помощью проверки параметрической гипотезы). В меню Сервис выберите команду Анализ данных, укажите инструмент анализа Гистограмма. Нажмите кнопку ОК. Значения параметров в появившемся диалоговом окне установите следующим образом: · Входной интервал — введите ссылки на ячейки С24: С44 (ячейки со значениями остатков и названием Остатки); · Интервал карманов — не заполняйте; · Метки — установите флажок; · Параметры вывода — установите переключатель на Новый рабочий лист и в поле напротив введите его название «Условие1-нормальность»; · Парето — оставьте пустым; · Интегральный процент — оставьте пустым; · Вывод графика — установите флажок. Нажмите ОК. Растяните гистограмму вниз. При необходимости ее можно перемещать. Для нахождения асимметрии и эксцесса и проверки гипотезы о нормальности распределения остатков найдите числовые характеристики остатков. Скопируйте ячейки С24: С44 листа «Регрессия» со значениями остатков и названием Остатки на лист «Условие1-нормальность» в ячейки С12: С32. Выберите в меню Сервис → Анализ данных → Описательная статистика, нажмите ОК. Значения параметров в диалоговом окне: · Входной интервал — введите ссылки на ячейки С12: С32; · Группирование — установите флажок по столбцам; · Метки в первой строке — установите флажок; · Параметры вывода – установите переключатель на Выходной интервал, курсор установите в поле напротив, выделите ячейку А12; · установите флажки Итоговая статистика, уровень надежности (95%). Нажмите ОК. Для проверки гипотезы о нормальности распределения остатков с помощью критерия хи-квадрат Пирсона сравниваются наблюдаемое и критическое значения статистики хи-квадрат. Рассчитайте наблюдаемое значение статистики c2 = На листе «Условие1-нормальность» удалите слово Еще в ячейке А6 и в этой же ячейке введите формулу =В24*3, нажмите Enter (т.е. значение максимума остатков увеличили в три раза). В ячейку С1 введите значение 0 — значение функции распределения на минус бесконечности. В ячейки С2: С6 введите формулу массива: 1) выделите ячейки С2: С6; 2) нажмите функциональную F2; 3) введите формулу =HOPMPACП(А2: А6; В14; В18; ИСТИНА); 4) нажмите комбинацию кнопок Ctrl+Shift+Enter. Если появилось только одно значение, то нажать F2 и снова Ctrl+Shift+Enter. В строке формул при активизации любой ячейки диапазона С2: С6 появится формула в фигурных скобках: {=HOPMPACП(А2: А6; В14; В18; ИСТИНА)} Замечание. В дальнейшем фраза «введите формулу массива» предполагает выполнение четырех действий: 1) выделить заполняемый диапазон ячеек; 2) нажать на клавиатуре кнопку F2; 3) ввести формулу; 4) нажать комбинацию кнопок Ctrl+Shift+Enter. В ячейки D2: D6 введите формулу массива {=С2: C6-С1: C5} (обратите внимание, во втором массиве ячейку C6 не включать). В ячейки Е2: E6 введите формулу массива {=В26*D2: D6}. В ячейки F2: F6 введите формулу массива {=(B2: В6-Е2: Е6)^2/Е2: E6}. В ячейку E7 введите обозначение хи-квадрат набл. В ячейку F7 введите формулу =СУММ(F2: F6) для вычисления хи-квадрат набл. Найдите критическое значение статистики Пирсона. В ячейку E8 введите обозначение хи-квадрат кр. В ячейку F8 введите формулу для вычисления хи-квадрат кр (используя Мастер функций – статистические) =ХИ2ОБР(0, 05; 6-2-1), где 6 — число интервалов (6 получено как сумма числа значений в кармане и 1). Замечание. Выводы о нормальности распределения остатков подробно описаны в разделе «Анализ эконометрической модели парной регрессии». 4.3. Значимость коэффициентов регрессии: проверка соответствующих гипотез. Для проверки гипотез о значимости коэффициентов регрессии сравниваются наблюдаемые значения t-статистики, найденные с помощью анализа Регрессия, и критическое значение, которое уже найдено на листе «Исходные данные». Для удобства дальнейшего анализа скопируйте содержимое ячеек D12: E12 листа «Исходные данные» в ячейки C19: D19 листа «Регрессия». Замечание. Выводы о значимости коэффициентов регрессии подробно описаны в разделе «Анализ эконометрической модели парной регрессии».
|

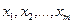 с помощью одного уравнения, в котором каждому конкретному набору (
с помощью одного уравнения, в котором каждому конкретному набору ( ) объясняющих факторов
) объясняющих факторов 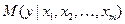 . Такая зависимость называется корреляционной. При этом модель называется парной, если уравнение связывает только две переменные
. Такая зависимость называется корреляционной. При этом модель называется парной, если уравнение связывает только две переменные  и описывается уравнением парной регрессии вида
и описывается уравнением парной регрессии вида 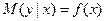 . Если же речь идет о зависимости величины y от нескольких факторов
. Если же речь идет о зависимости величины y от нескольких факторов  ), то модель с одним уравнением
), то модель с одним уравнением 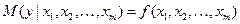 называется множественной моделью. В зависимости от вида функции, эконометрические модели разделяются на линейные и нелинейные.
называется множественной моделью. В зависимости от вида функции, эконометрические модели разделяются на линейные и нелинейные.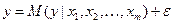 .
.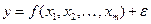 называется регрессионной моделью (или уравнением регрессионной модели).
называется регрессионной моделью (или уравнением регрессионной модели).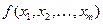 такова, что наиболее точно соответствует данным наблюдений.
такова, что наиболее точно соответствует данным наблюдений. . Спрогнозировать объем экспорта при ВВП, равном 2500 ед.
. Спрогнозировать объем экспорта при ВВП, равном 2500 ед. и критическое
и критическое  значения статистики Стьюдента, для нахождения которых выполните следующие действия.
значения статистики Стьюдента, для нахождения которых выполните следующие действия. парной линейной регрессионной модели
парной линейной регрессионной модели  , где
, где 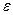 – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, выполнив следующие действия.
– случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, выполнив следующие действия. , которое вычислите на листе «Регрессия» в ячейке E15 следующим образом:
, которое вычислите на листе «Регрессия» в ячейке E15 следующим образом: , выполнив следующие несколько действий.
, выполнив следующие несколько действий.


