Прогнозирование. Если выполняются все условия верификации, то модель является качественной
Так как выполняются все условия верификации, то модель является качественной. Таким образом, прогноз, выполненный по ней, является качественным: несмещенным, состоятельным и эффективным. На листе «Регрессия» для заданного значения ВВП, равного 2500, рассчитан точечный прогноз экспорта, который равен 575, и интервальный прогноз, равный (539, 04, 610, 96). Этот доверительный интервал значений экспорта содержит с вероятностью 0, 95 истинное значение экспорта при заданном значении ВВП. Вопросы для самоконтроля 1. Перечислите этапы построения эконометрической модели. 2. Кратко охарактеризуйте цель каждого этапа. 3. Знания из каких научных дисциплин необходимы на каждом из этапов эконометрического моделирования? 4. В чем состоит спецификация модели парной регрессии? 5. Почему в уравнении регрессии присутствует случайная переменная? 6. Как определить силу и направленность взаимодействия факторов? 7. Что означает положительная ковариация между исследуемыми факторами? 8. Что означает отрицательная корреляция между исследуемыми факторами? 9. Как может быть представлено графически взаимодействие факторов? 10. Что означает значимость коэффициента корреляции? 11. Как проверить на значимость коэффициент корреляции? 12. В чем суть метода наименьших квадратов (МНК) для нахождения оценок параметров регрессии? 13. Почему с помощью МНК находятся оценки параметров, а не их точные значения? 14. Какая оценка параметра называется точечной? 15. В чем суть интервальной оценки параметров? 16. Как найти интервальные оценки коэффициентов регрессии? 17. Как используются стандартные ошибки регрессии и стандартные ошибки коэффициентов регрессии при анализе оценок параметров парной регрессии? 18. В чем экономический смысл параметров модели парной регресии? 19. Как можно оценить общее качество уравнения регрессии? 20. Объясните суть коэффициента детерминации, нормированного коэффициента детерминации. В каких пределах они изменяются? 21. Какова связь между коэффициентом детерминации, коэффициентом корреляции и множественным коэффициентом корреляции для парной регрессии? 22. Для какой цели в парной регрессии используется критерий Фишера? 23. Как получить остатки для модели парной регрессии? 24. Какому условию должны удовлетворять остатки, чтобы для проверки статистических гипотез можно было использовать критерий Стьюдента? 25. Какое распределение называется нормальным? Каковы его параметры? 26. Какими способами можно проверить нормальность распределения остатков? 27. Запишите уравнение плотности распределения остатков для Вашего варианта. 28. Изобразите кривую плотности распределения остатков для Вашего варианта. 29. Каковы значения асимметрии и эксцесса для нормально распределенной случайной величины? 30. Как используется критерий согласия Пирсона для проверки гипотезы о нормальном законе распределения остатков? 31. Для чего проверяется значимость коэффициентов регрессии? 32. В чем суть статистической значимости коэффициентов регрессии? 33. Какими свойствами должны обладать оценки параметров регрессии? 34. Сформулируйте основные предпосылки применения МНК для построения регрессионной модели. 35. Каковы последствия невыполнимости предпосылок применения МНК? 36. Сформулируйте теорему Гаусса-Маркова? 37. Как проверить центрированность остатков (условие 1) теоремы Гаусса-Маркова? 38. В чем суть гетероскедастичности остатков? 39. Каковы причины гетероскедастичности остатков? 40. Каковы последствия гетероскедастичности остатков? 41. Как определить гомоскедастичность остатков визуально? 42. Для чего и как используется тест ранговой корреляции Спирмена? 43. В чем суть автокорреляции остатков и каковы ее последствия? 44. Назовите методы определения автокорреляции остатков. 45. Как проверить гипотезу об отсутствии автокорреляции остатков с помощью критерия Дарбина-Уотсона. 46. Как проверить гипотезу об отсутствии автокорреляции остатков визуально? 47. Что характеризует коэффициент эластичности? 48. Что такое прогнозирование? 49. Как получить точечный прогноз зависимого фактора? 50. Как получить интервальный прогноз зависимого фактора?
Индивидуальные задания Исследовать зависимость объема экспорта (y, усл. ед.) от валового внутреннего продукта (ВВП) (x, усл. ед.), используя данные 20 наблюдений, приведенные в таблице 1.1, которые необходимо изменить следующим образом: к каждому значению ВВП таблицы 1.1 надо прибавить 12* к, где к – номер студента в журнале группы. Построитьрегрессионную модель
ТЕМА 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ Постановка задачи Исследовать зависимость заработной платы (
Таблица 2.1 – Данные наблюдений
Технология вычислений в Excel для построения и анализа линейной множественной регрессии Замечание. Вычисления на каждом этапе эконометрического моделирования линейной множественной регрессии аналогичны проведенным в теме 1. Поэтому суть каждого этапа не приводится. 1. Постановочный этап. Введите исходные данные (таб. 2.1). Для этого в ячейку А1 введите название первого столбца — «ЗП», в ячейку В1 — название второго столбца — «Возраст», в ячейку C1 — название третьего столбца — «Стаж». В ячейки А2, А3, …, А21 введите данные первого столбца таблицы 2.1, в ячейки В2, В3, …, В21 — данные второго столбца, в ячейки C2, C3, …, С21 — данные третьего столбца. Введите новое название листа – «Исходные данные». Сохраните рабочую книгу (Файл → Сохранить как → …). 2. Спецификация. На листе «Исходные данные» выберите меню Сервис → Анализ данных → Корреляция → ОК. Значения параметров окна: Входной интервал – ячейки A1: С21, Метки — установите флажок, Параметры вывода – Выходной интервал, ссылка на ячейку Е2. Нажмите ОК. Скопируйте G5 в H4. В ячейку Е1 введите Корреляционная матрица. В ячейку Е6 введите название Значимость коэффициентов корреляции. В ячейку Е7 введите обозначение tЗП, В набл. В ячейку F7 введите =F4*КОРЕНЬ((20-2)/(1-F4^2)) — формула для вычисления tнабл для коэффициента корреляции факторов ЗП и возраст, где 20 — число наблюдений, 2 — число факторов. В ячейку Е8 введите tЗП, С набл. В ячейку F8 введите =F5*КОРЕНЬ((20-2)/(1-F5^2)) — формула для вычисления tнабл для коэффициента корреляции факторов ЗП и стаж, где 20 — число наблюдений, 2 — число факторов. В ячейку Е9 введите tкр. В ячейке F9 вычислите критическое значение tкр следующим образом: – нажмите на fx (вставка функций); – в поле «Категория» окна Мастер функций выберите статистические, из предложенных ниже функций выделите СТЬЮДРАСПОБР и нажмите ОК. Откроется окно «Аргументы функций». Заполните поля: · Вероятность — наберите значение 0, 05; · Степени свободы — введите 20-2, где 20 — число наблюдений, 2 — число факторов. Нажмите ОК.
|

 зависимой переменной определяется путем подстановки в найденное уравнение регрессии заданного допустимого значения независимой переменной
зависимой переменной определяется путем подстановки в найденное уравнение регрессии заданного допустимого значения независимой переменной  .
Интервальный прогноз или доверительный интервал прогноза имеет вид:
.
Интервальный прогноз или доверительный интервал прогноза имеет вид:
 ,
где
,
где  – критическое значение
– критическое значение  -статистики при заданном уровне значимости
-статистики при заданном уровне значимости  и числе степеней свободы
и числе степеней свободы  ,
,  – средняя стандартная ошибка прогноза, S — стандартная ошибка регрессии,
– средняя стандартная ошибка прогноза, S — стандартная ошибка регрессии,  – исправленная дисперсия независимой переменной x.
– исправленная дисперсия независимой переменной x.
 . Спрогнозировать объем экспорта при ВВП, равном 1970 усл. ед.
. Спрогнозировать объем экспорта при ВВП, равном 1970 усл. ед.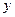 , тыс. руб.) от возраста (
, тыс. руб.) от возраста ( , лет) и стажа по данной специальности (
, лет) и стажа по данной специальности ( , лет), используя данные наблюдений, приведенные в таблице 2.1. Построить регрессионную модель
, лет), используя данные наблюдений, приведенные в таблице 2.1. Построить регрессионную модель  . Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.
. Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.


