Частные коэффициенты корреляции.

Коэффициент частной корреляции первого порядка для переменной 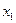при неизменном значении переменной 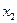находится по формуле (через коэффициенты парной корреляции факторов). Для его нахождения выполните следующие действия:

в ячейку E16 введите название Частные коэф. корр.;

в ячейку E17 введите название rЗП, В-С;

в ячейку F17 введите формулу =(F4-F5*G5)/КОРЕНЬ((1-F5^2)*(1-G5^2)).

Аналогично найдите :

в ячейку E18 введите название rЗП, С-В;

в ячейку F18 введите формулу =(F5-F4*G5)/КОРЕНЬ((1-F4^2)*(1-G5^2)).

Проверка значимости частных коэффициентов осуществляется сравнением наблюдаемых и критического значений t-статистики аналогично проверке значимости парных коэффициентов корреляции на этапе спецификации (см. выше).

 

5. Прогнозирование. На листе «Регрессия» в ячейке Е1 введите название Точечный прогноз, в ячейку Е2 введите формулу =В17+В18*35+В19*10 для расчета точечной оценки заработной платы при возрасте работника 35 лет и стаже работы 10 лет из условия задачи.

Замечание. Стандартная ошибка прогноза считается по формуле , где Х – матрица наблюдений независимых переменных, Х_р – матрица значений независимых переменных для прогноза, S – стандартная ошибка регрессии, Т – операция транспонирования матрицы.

В ячейку В2 нового листа «Интервальный_прогноз» скопируйте ячейки В2: С21 листа «Исходные данные». Заполните ячейки А2: А21 единицами (это значения переменной при свободном член). Для простоты дальнейших ссылок в объединенные ячейки А1: С1 введите название Массив 1 (массив Х, содержащий значения переменной при свободном члене, возраста, стажа – ячейки A2: C21), в ячейку D1 – Массив 2 (массив Хр, содержащий данные для прогноза – ячейки D2: D4). В ячейку D2 введите 1, в D3 – 35 (возраст), в D4 – 10 (стаж).

Пример оформления промежуточных вычислений стандартной ошибки прогноза и интервального прогноза приведен на рисунке 2.1.

Для транспонирования массива 2 введите в ячейки А23: С23 формулу массива {=ТРАНСП(D2: D4)}

Для транспонирования массива 1 введите в ячейки A25: Т27 формулу массива {=ТРАНСП(A2: C21)}.

Результатом произведения транспонированного массива 1 размерностью 3 на 20 и массива 1 размерностью 20 на 3 является массив 3 размерностью 3 на 3, поэтому в ячейки А29: С31 введите формулу массива {=МУМНОЖ(A25: T27; A2: C21)}.

Результатом вычисления обратной матрицы полученного массива 3, является матрица размерностью 3 на 3, которая находится в ячейках А33: С35 по формуле массива {=МОБР(A29: C31)} (массив 4).

Результатом произведения транспонированного массива 2 размерностью 1 на 3 и массива 4 размерностью 3 на 3 является массив 5 размерностью 1 на 3, поэтому в ячейки А37: С37 введите формулу массива {=МУМНОЖ(A23: C23; A33: C35)}.

Результатом произведения массива 5 размерностью 1 на 3 и массива 2 размерностью 3 на 1 является массив 6 размерностью 1 на 1, поэтому в ячейку А39 введите формулу =МУМНОЖ(A37: C37; D2: D4).

Стандартную ошибку прогноза посчитайте в ячейке А41 по формуле =регрессия! B7*КОРЕНЬ(A39).

Интервальный прогноз величины заработной платы рассчитайте в ячейках А43, В43 соответственно по формулам:

='регрессия'! E2-регрессия! D20*'Интервальный_прогноз'! A41

для левого конца интервала,

='регрессия'! E2+'регрессия'! D20*'Интервальный_прогноз'! A41

для правого конца интервала.

Замечание. Запись 'регрессия'! Е2 означает, что ячейка Е2 находится на листе «регрессия». Набор и редактирование формулы осуществляется в строке формул.

 

а)

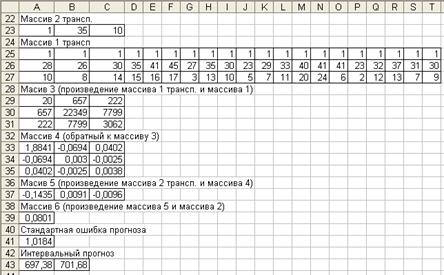
б)

Рисунок 2.1 – Пример оформления вычислений интервальной оценки прогноза: а) исходные данные; б) вычисления.

Анализ эконометрической модели множественной линейной регрессии