Верификация модели. 4.1. Общее качество уравнения.Оценим общее качество модели по коэффициенту (индексу) детерминации и нормированному индексу детерминации (см
4.1. Общее качество уравнения. Оценим общее качество модели по коэффициенту (индексу) детерминации и нормированному индексу детерминации (см. в п 4.1 анализа темы 1). Проанализируем показатели в таблице Регрессионная статистика листа «Регрессия» (таблица 2.5). Таблица 2.5 – Регрессионная статистика
Коэффициент множественной детерминации R-квадрат равен 0, 9964. Так как он близок к 1, то уравнение имеет высокое качество. Этот факт подтверждает также нормированный индекс множественной детерминации, равный 0, 996. В таблице Дисперсионный анализ листа «Регрессия» рассчитаны наблюдаемое и критическое значения критерия Фишера (таблица 2.6). Таблица 2.6 – Дисперсионный анализ
Так как наблюдаемое значение Fнабл =2392, 35 > Fкр = 3, 59, то R-квадрат значим, что еще раз подтверждает высокое качество построенного уравнения линейной множественной регрессии.
4.2. Нормальность распределения остатков. Проанализируем нормальность распределения остатков по: 1) гистограмме остатков, 2) числовым характеристикам асимметрии и эксцессу, 3) критерию Пирсона.
1) Построим гистограмму остатков. Соединим середины верхних сторон прямоугольников гистограммы и получим полигон распределения, по которому визуально можно предположить закон распределения.
Рисунок 2.2 – Гистограмма
Так как ломаная линия на рис. 2.2 близка к кривой нормального распределения, заданной уравнением 2) Асимметричность равна -0, 36 (левосторонняя асимметричность эмпирической кривой относительно теоретической), эксцесс равен 0, 1 («островершинность» эмпирической кривой), то есть характеристики плотности распределения асимметричность и эксцесс незначительно отличаются от нуля, поэтому можно считать распределение нормальным. 3) Подтвердим нормальность распределения с помощью критерия Пирсона. На листе «Регрессия»найдены наблюдаемое и критическое значения статистики хи-квадрат (таблица 2.7). Таблица 2.7 – Проверка критерия Пирсона
Наблюдаемое значение, равное 3, 16, меньше хи-квадрат критического, равного 7, 81, поэтому остатки распределеныпо нормальному закону. 4.3. Значимость коэффициентов регрессии. Проверим значимость коэффициентов регрессии.
Значимость коэффициентов регрессии оценивается с помощью Наблюдаемое значение статистики для коэффициента Аналогично, для коэффициента Значимость коэффициентов регрессии подтверждает выдвинутое на этапе спецификации предположение о линейной форме зависимости факторов.
|






 (сравните с рис. 1.2), то остатки распределены по нормальному закону. Следовательно, по визуальному анализу гистограммы можно предположить нормальность распределения остатков.
(сравните с рис. 1.2), то остатки распределены по нормальному закону. Следовательно, по визуальному анализу гистограммы можно предположить нормальность распределения остатков. –статистики, значения которой получены на листе «Регрессия» (см. таблицу 2.4).
–статистики, значения которой получены на листе «Регрессия» (см. таблицу 2.4).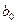 tнабл = 115, 59 (оно равно отношению точечной оценки коэффициента
tнабл = 115, 59 (оно равно отношению точечной оценки коэффициента 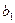 имеем tнабл = 5, 26, tкр = 2, 1, Так как |tнабл| =5, 26 > tкр = 2, 1, поэтому коэффициент
имеем tнабл = 5, 26, tкр = 2, 1, Так как |tнабл| =5, 26 > tкр = 2, 1, поэтому коэффициент  имеем |tнабл| =41, 85 > tкр = 2, 1, поэтому коэффициент
имеем |tнабл| =41, 85 > tкр = 2, 1, поэтому коэффициент 


