Если выполняются все условия верификации, то модель является качественной. В противном случае ее надо усовершенствовать: либо на этапе спецификации, либо варьировать выборку. По качественной модели можно прогнозировать значение зависимой переменной при заданных значениях независимых переменных. Точечный прогноз получается подстановкой заданных значений независимых переменных в уравнение регрессии. Интервальный прогноз – это интервал значений зависимой переменной, содержащий с вероятностью 0, 95 истинное ее значение при заданных значениях независимых переменных. Центр интервала равен точечному прогнозу, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки прогноза на критическое значение t-статистики, т. е.  . Средняя стандартная ошибка прогноза . Средняя стандартная ошибка прогноза  в матричной форме имеет вид: в матричной форме имеет вид:
 ,
где S — стандартная ошибка регрессии, ,
где S — стандартная ошибка регрессии,  – матрица заданных для построения прогноза значений независимых переменных – матрица заданных для построения прогноза значений независимых переменных  , ,  , ,  – матрица, составленная из столбца n единиц, столбца n значений переменной – матрица, составленная из столбца n единиц, столбца n значений переменной 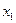 и столбца n значений переменной и столбца n значений переменной  из исходных данных, индекс Т обозначает операцию транспонирования матрицы. из исходных данных, индекс Т обозначает операцию транспонирования матрицы.
|
Так как выполняются все условия верификации, то модель является качественной, следовательно, прогноз, выполненный по ней является качественным: несмещенным, состоятельным и эффективным. На листе «Регрессия»рассчитан точечный прогноз заработной платы, который равен 699, 53, на листе Интервальный прогноз получен интервальный прогноз (697, 38; 701, 68), который означает, что с вероятностью 0, 95 любое значение из этого интервала является оценкой заработной платы.
Вопросы для самоконтроля
- Перечислите этапы построения эконометрической модели.
- Кратко охарактеризуйте цель каждого этапа.
- Знания из каких научных дисциплин необходимы на каждом из этапов эконометрического моделирования?
- В чем состоит спецификация модели множественной регрессии?
- Почему в уравнении регрессии присутствует случайная переменная?
- Как определить силу и направленность взаимодействия факторов?
- Что означает значимость коэффициента корреляции?
- Как проверить на значимость коэффициент корреляции?
- В чем суть метода наименьших квадратов (МНК) для нахождения оценок параметров регрессии?
- Почему с помощью МНК находятся оценки параметров, а не их точные значения?
- Какая оценка параметра называется точечной?
- В чем суть интервальной оценки параметров?
- Как найти интервальные оценки коэффициентов регрессии?
- Как используются стандартные ошибки регрессии и стандартные ошибки коэффициентов регрессии при анализе оценок параметров регрессии?
- В чем экономический смысл параметров модели регресии?
- Как можно оценить общее качество уравнения регрессии?
- Объясните суть коэффициента детерминации, нормированного коэффициента детерминации. В каких пределах они изменяются?
- Какова связь между коэффициентом детерминации, коэффициентом корреляции и множественным коэффициентом корреляции для множественной регрессии?
- Для какой цели в парной регрессии используется критерий Фишера?
- Как получить остатки для модели парной регрессии?
- Какому условию должны удовлетворять остатки, чтобы для проверки статистических гипотез можно было использовать критерий Стьюдента?
- Какое распределение называется нормальным? Каковы его параметры?
- Какими способами можно проверить нормальность распределения остатков?
- Как используется критерий согласия Пирсона для проверки гипотезы о нормальном законе распределения остатков?
- Для чего и как проверяется значимость коэффициентов регрессии?
- Какими свойствами должны обладать оценки параметров регрессии?
- Сформулируйте основные предпосылки применения МНК для построения регрессионной модели.
- Каковы последствия невыполнимости предпосылок применения МНК?
- Сформулируйте теорему Гаусса-Маркова?
- Как проверить центрированность остатков?
- В чем суть гетероскедастичности (гомоскедастичность) остатков?
- Каковы причины и последствия гетероскедастичности остатков?
- Как определить гомоскедастичность остатков?
- В чем суть автокорреляции остатков и каковы ее последствия?
- Как проверить гипотезу об отсутствии автокорреляции остатков с помощью критерия Дарбина-Уотсона?
- Как проверить гипотезу об отсутствии автокорреляции остатков визуально?
37. Что характеризуют средние коэффициенты эластичности?
38. Для чего используются частные коэффициенты корреляции и как они рассчитываются?
39. Каковы последствия мультиколлинеарности остатков?
- Что такое прогнозирование?
- Как получить точечный прогноз зависимого фактора?
- Как получить интервальный прогноз зависимого фактора?
Индивидуальные задания
Исследовать зависимость заработной платы (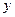 , тыс. руб.) от возраста (
, тыс. руб.) от возраста ( , лет) и стажа по данной специальности (
, лет) и стажа по данной специальности ( , лет), используя данные наблюдений, приведенные в таблице 2.1, прибавив к заработной плате значение 10* к, где к – номер в журнале. Построить регрессионную модель
, лет), используя данные наблюдений, приведенные в таблице 2.1, прибавив к заработной плате значение 10* к, где к – номер в журнале. Построить регрессионную модель  . Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.
. Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.
ТЕМА 3. ВРЕМЕННЫЕ РЯДЫ
Постановка задачи
Динамика выпуска продукции некоторого предприятия характеризуется данными, представленными в таблице:
Таблица 3.1 – Исходные данные
| год
| выпуск продукции
(млн. руб.)
| год
| выпуск продукции
(млн. руб.)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проанализируйте структуру временного ряда, проверьте гипотезу о структурной стабильности ряда, проведите аналитическое выравнивание временного ряда, сделайте прогноз на 2011 год.
Технология вычислений в Excel при построении модели временного ряда.
1. Постановочный этап. Введите подготовленные исходные данные. В ячейку А1 введите название первого столбца — «Год», в ячейку В1 — название второго столбца — «Выпуск продукции». В ячейки А2, А3, …, А21 введите данные первого столбца исходной таблицы, в ячейки В2, В3, …, В21 — данные второго столбца согласно варианту.
Введите новое название листа «Исходные данные. Сохраните рабочую книгу под названием «Временные ряды».
2. Спецификация: определение вида аналитической модели временного ряда.

 . Средняя стандартная ошибка прогноза
. Средняя стандартная ошибка прогноза  в матричной форме имеет вид:
в матричной форме имеет вид:
 ,
где S — стандартная ошибка регрессии,
,
где S — стандартная ошибка регрессии,  – матрица заданных для построения прогноза значений независимых переменных
– матрица заданных для построения прогноза значений независимых переменных  ,
,  ,
,  – матрица, составленная из столбца n единиц, столбца n значений переменной
– матрица, составленная из столбца n единиц, столбца n значений переменной 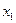 и столбца n значений переменной
и столбца n значений переменной  из исходных данных, индекс Т обозначает операцию транспонирования матрицы.
из исходных данных, индекс Т обозначает операцию транспонирования матрицы.
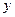 , тыс. руб.) от возраста (
, тыс. руб.) от возраста ( , лет) и стажа по данной специальности (
, лет) и стажа по данной специальности ( . Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.
. Рассчитать значение заработной платы для работника в возрасте 35 лет со стажем работы по данной специальности 10 лет.


