Постановочный этап
Из экономической теории известно, что заработная плата зависит от многих факторов, например, от возраста, квалификации, стажа по данной специальности, общего стажа работы, производительности труда и т. д. Выделим два фактора – возраст и стаж по данной специальности, которые являются объясняющими факторами для результативного (объясняемого) фактора – заработная плата (ЗП). Поэтому возникает задача количественного описания зависимости указанных экономических показателей уравнением множественной регрессии 2. Спецификация модели. Определим наличие зависимости показателя Заработная плата от Возраста и Стажа, а также форму этой зависимости.
На листе «Исходные данные» получена следующая таблица: Таблица 2.2 – Корреляционная матрица
Коэффициент корреляции ЗП и возраст равен 0, 795 > 0, поэтому зависимость между ними прямая и высокая. Коэффициент корреляции ЗП и стаж равен 0, 995 > 0, поэтому зависимость между ними прямая и весьма высокая (таб. 1.2). Проверим на значимость коэффициенты парной корреляции. На листе «Исходные данные» вычислены наблюдаемые и критическое значения t-статистики (таблица 2.3).
Таблица 2.3 – Значимость коэффициентов корреляции
Так как |tЗП, В набл| = 5, 56 > tкр = 2, 1, то коэффициент корреляции значим (значительно отличается от нуля). Поэтому подтверждается наличие линейной зависимости между факторами ЗП и возраст. Так как |tЗП, С набл| = 43, 79 > tкр = 2, 1, то коэффициент корреляции значим. Поэтому также подтверждается наличие линейной зависимости между факторами ЗП и стаж. Исходя из проведенного анализа можно выдвинуть предположение о том, что зависимость заработной платы 3. Параметризация модели. Найдем оценки неизвестных параметров модели.
В результате проведения регрессионного анализа на листе «Регрессия»получены точечные и интервальные оценки неизвестных параметров модели (таблица 2.4).
Таблица 2.4 – Статистика коэффициентов регрессии
Точечная оценка параметра Точечная оценка параметра Точечная оценка параметра Таким образом, уравнение регрессии имеет вид y = 570, 74 + 1, 03 Так как любое значение из доверительного интервала может служить оценкой параметра, то уравнение регрессии также может иметь вид: y = 568 + 0, 8
|

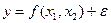 на основе 20 наблюдений экономических показателей.
на основе 20 наблюдений экономических показателей. (см. тему 1).
(см. тему 1).
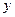 от возраста (
от возраста ( ) и стажа (
) и стажа ( ) по данной специальности описывается линейной регрессионной моделью
) по данной специальности описывается линейной регрессионной моделью  , где
, где  – неизвестные параметры модели,
– неизвестные параметры модели, 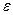 – случайный член, который включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений.
– случайный член, который включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений. множественной регрессии имеет такой же вид, как и для
множественной регрессии имеет такой же вид, как и для  в теме 1.
в теме 1.
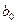 (Y-пересечение) равна 570, 74, ее интервальная оценка равна (560, 32; 581, 16).
(Y-пересечение) равна 570, 74, ее интервальная оценка равна (560, 32; 581, 16).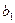 при переменной
при переменной 


