4.5.1. Мультиколлинеарность факторов. Проверим мультиколлинеарность факторов.
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной, линейной связанности. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если их парный коэффициент корреляции больше или равен 0, 7. При наличии мультиколлинеарности МНК-оценки формально существуют, но обладают рядом недостатков. В частности, оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой с высоким значением коэффициента детерминации.
Для отбора факторов в модель регрессии можно использовать корреляционную матрицу. Однако по величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Поэтому при оценке мультиколлинеарности факторов предполагается использовать определитель  матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0, т. е. матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0, т. е.  . Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Мультиколлинерность факторов выявляется проверкой гипотезы . Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Мультиколлинерность факторов выявляется проверкой гипотезы  с помощью статистики хи-квадрат с с помощью статистики хи-квадрат с  степенями свободы. Наблюдаемое значение статистики определяется по формуле степенями свободы. Наблюдаемое значение статистики определяется по формуле  , где n – количество наблюдений, p – число переменных. Если , где n – количество наблюдений, p – число переменных. Если  , то гипотеза , то гипотеза  отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной. отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной.
|
На листе «Исходные данные» найдены парные коэффициенты корреляции и определитель матрицы парных коэффициентов корреляции объясняющих факторов Возраст и Стаж. Так как парный коэффициент корреляции  =0, 75 < 0, 8, то зависимость между факторами существует, но она незначительная. Докажем это предположение проверкой гипотезы об отсутствии мультиколлинеарности с помощью статистики хи-квадрат, наблюдаемое и критическое значения которой найдены на листе «Регрессия» (таблица 2.5).
=0, 75 < 0, 8, то зависимость между факторами существует, но она незначительная. Докажем это предположение проверкой гипотезы об отсутствии мультиколлинеарности с помощью статистики хи-квадрат, наблюдаемое и критическое значения которой найдены на листе «Регрессия» (таблица 2.5).
Таблица 2.5 – Мультиколлинеарность.
| Мультиколлинеарность
|
| Определитель
| 0, 440603872
|
| хи-кв набл
| 19, 53392754
|
| хи-кв кр
| 223, 160247
|
Так как хи-квадрат наблюдаемое равно 19, 53 и меньше хи-квадрат критического, равного 223, 16, то мультиколлинеарность факторов отсутствует.
4.5.2. Эластичность. Оценим влияние каждого объясняющего фактора на результирующий фактор ЗП.
Частные средние коэффициенты эластичности показывают, на сколько процентов от среднего значения изменяется зависимая переменная с изменением на 1% фактора 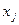 от своего среднего при фиксированном значении других факторов. Частные коэффициенты эластичности по каждой объясняющей переменной для линейной регрессии рассчитывается по формуле: от своего среднего при фиксированном значении других факторов. Частные коэффициенты эластичности по каждой объясняющей переменной для линейной регрессии рассчитывается по формуле:  . .
|
На листе «Исходные данные» найдены коэффициенты эластичности факторов возраст и стаж (таблица 2.6).
Таблица 2.6 – Эластичность факторов
| Эластичность
|
| ЗП_ср
| Возраст_ср
| Стаж_ср
|
| 707, 5215
| 32, 85
| 11, 1
|
| Коэф. регрессии Возраст
| 1, 029555
|
|
| Коэф. эласт.фактора Возраст
| 0, 047802
|
|
| Коэф. регрессии Стаж
| 9, 275783
|
|
| Коэф. эласт. фактора Стаж
| 0, 145524
|
|
С изменением значения фактора Возраст на 1% при фиксированном значении фактора Стаж значение фактора ЗП увеличивается на 0, 05%. Аналогично, с изменением значения фактора стаж на 1% при фиксированном значении фактора возраст значение фактора ЗП увеличивается на 0, 15%. Значит, влияние фактора Стаж больше чем фактора Возраст.
4.5.3. Частные коэффициенты корреляции: целесообразность включения в модель факторов. Определим степень влияния факторов на результирующий фактор ЗП при устранении влияния других факторов.
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при неизменном уровне других факторов, включенных в уравнение регрессии. Они широко используются при решении проблемы отбора факторов, ранжировании факторов, участвующих в множественной линейной регрессии. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например,  — коэффициент частной корреляции первого порядка для переменной — коэффициент частной корреляции первого порядка для переменной 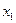 при неизменном значении переменной при неизменном значении переменной 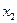 . Аналогично определяется . Аналогично определяется  через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью  -статистики -статистики  , которая имеет распределение Стьюдента. Если , которая имеет распределение Стьюдента. Если 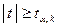 , то проверяемый коэффициент значим. , то проверяемый коэффициент значим.
|
На листе «Исходные данные» найдены частные коэффициенты корреляции
Таблица 2.7 – Частные коэффициенты корреляции
| Частные коэф. коррел.
| Значимость
|
|
| rЗП, В-С
| 0, 787011734
| tнаблrЗП, В-С
| 5, 412226
|
| rЗП, С-В
| 0, 995181352
| tнаблrЗП, С-В
| 43, 06106
|
Так как 0, 78 < 0, 99, то из двух факторов большее влияние оказывает фактор стаж.
Оба частных коэффициента корреляции значимы: |tнаблЗП, В-С| = 5, 4 > tкр = 2, 1, |tнаблЗП, С-В| = 43, 06 > tкр = 2, 1.

 матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0, т. е.
матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0, т. е.  . Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Мультиколлинерность факторов выявляется проверкой гипотезы
. Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Мультиколлинерность факторов выявляется проверкой гипотезы  с помощью статистики хи-квадрат с
с помощью статистики хи-квадрат с  степенями свободы. Наблюдаемое значение статистики определяется по формуле
степенями свободы. Наблюдаемое значение статистики определяется по формуле  , где n – количество наблюдений, p – число переменных. Если
, где n – количество наблюдений, p – число переменных. Если  , то гипотеза
, то гипотеза  отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной.
отклоняется и наличие мультиколлинеарности объясняющих факторов считается доказанной.
 =0, 75 < 0, 8, то зависимость между факторами существует, но она незначительная. Докажем это предположение проверкой гипотезы об отсутствии мультиколлинеарности с помощью статистики хи-квадрат, наблюдаемое и критическое значения которой найдены на листе «Регрессия» (таблица 2.5).
=0, 75 < 0, 8, то зависимость между факторами существует, но она незначительная. Докажем это предположение проверкой гипотезы об отсутствии мультиколлинеарности с помощью статистики хи-квадрат, наблюдаемое и критическое значения которой найдены на листе «Регрессия» (таблица 2.5).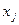 от своего среднего при фиксированном значении других факторов. Частные коэффициенты эластичности по каждой объясняющей переменной для линейной регрессии рассчитывается по формуле:
от своего среднего при фиксированном значении других факторов. Частные коэффициенты эластичности по каждой объясняющей переменной для линейной регрессии рассчитывается по формуле:  .
.
 — коэффициент частной корреляции первого порядка для переменной
— коэффициент частной корреляции первого порядка для переменной 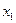 при неизменном значении переменной
при неизменном значении переменной 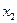 . Аналогично определяется
. Аналогично определяется  через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью
через коэффициенты парной корреляции факторов.
Значимость частных коэффициентов корреляции оценивается с помощью  -статистики
-статистики  , которая имеет распределение Стьюдента. Если
, которая имеет распределение Стьюдента. Если 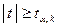 , то проверяемый коэффициент значим.
, то проверяемый коэффициент значим.



