| Корреляционным полем временного ряда называется множество точек на плоскости с координатами (t, y). По виду корреляционного поля оценивается тенденция, характеризующая совокупное долговременное воздействие множества факторов на динамику изучаемого показателя, которые в совокупности формируют его возрастание или убывание или их отсутствие.
|

Рисунок 3.1 – Корреляционное поле временного ряда
По виду корреляционного поля временной ряд содержит возрастающую тенденцию.
2.1.2. Оценка структуры временного ряда: наличие тренда, сезонности, цикличности, случайной компоненты – по автокорреляционной функции временного ряда и коррелограмме.
При наличии тенденции значение каждого последующего уровня ряда зависят от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями  исходного временного ряда и уровнями исходного временного ряда и уровнями  этого ряда, сдвинутыми на этого ряда, сдвинутыми на  шагов во времени, по следующей формуле: шагов во времени, по следующей формуле:
 ,
где ,
где  .
Число периодов .
Число периодов  , по которым рассчитывается коэффициент автокорреляции, называется лагом. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило: максимальный лаг должен быть не больше n/4.
Коэффициент автокорреляции является аналогом линейного коэффициента корреляции, изменяется в пределах от -1 до 1. Его значимость оценивается с помощью , по которым рассчитывается коэффициент автокорреляции, называется лагом. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило: максимальный лаг должен быть не больше n/4.
Коэффициент автокорреляции является аналогом линейного коэффициента корреляции, изменяется в пределах от -1 до 1. Его значимость оценивается с помощью  – статистики: – статистики:  , которая имеет распределение Стьюдента с , которая имеет распределение Стьюдента с  степенями свободы. Если степенями свободы. Если 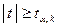 , то проверяемый коэффициент значим.
На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда.Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка , то проверяемый коэффициент значим.
На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда.Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка  , ряд содержит циклические колебания с периодичностью , ряд содержит циклические колебания с периодичностью  . Если ни один из коэффициентов автокорреляции не является значимым, можно сделать предположение относительно структуры этого ряда: ряд не содержит тренда и циклических колебаний, а только случайную компоненту.
По коэффициенту автокорреляции можно судить о наличии линейного тренда. Если временной ряд имеет сильную нелинейную тенденцию, то коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от; величины лага (порядка коэффициента автокорреляции) называется коррелограммой. При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда. . Если ни один из коэффициентов автокорреляции не является значимым, можно сделать предположение относительно структуры этого ряда: ряд не содержит тренда и циклических колебаний, а только случайную компоненту.
По коэффициенту автокорреляции можно судить о наличии линейного тренда. Если временной ряд имеет сильную нелинейную тенденцию, то коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от; величины лага (порядка коэффициента автокорреляции) называется коррелограммой. При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
|
Так как максимальным является коэффициент автокорреляции первого порядка (см. таблицу 3.2 и рис. 3.2), то исследуемый ряд не содержит сезонной компоненты, т. е. содержит только тренд и случайную структурные компоненты.
Таблица 3.2 – Значения автокорреляционной функции
| Период
| Коэф. автокор.
|
|
| 0, 988834449
|
|
| 0, 98120338
|
|
| 0, 975889226
|
|
| 0, 965213689
|
|
| 0, 965802478
|

Рисунок 3.2 – Автокорреляционная функция
Так как все наблюдаемые значения t-статистики больше критического (таблица 3.3), то все коэффициенты автокорреляции значимы. Это подтверждает предположение о том, что ряд содержит тренд и случайную компоненты.
Таблица 3.3 – Значимость коэффициентов автокорреляции
| Значимость
|
| t1
| 28, 15273
|
| t2
| 21, 57202
|
| t3
| 18, 96924
|
| t4
| 15, 66212
|
| t5
| 15, 80365
|
| tкр
| 2, 100922
|


 исходного временного ряда и уровнями
исходного временного ряда и уровнями  этого ряда, сдвинутыми на
этого ряда, сдвинутыми на  шагов во времени, по следующей формуле:
шагов во времени, по следующей формуле:
 ,
где
,
где  .
Число периодов
.
Число периодов  – статистики:
– статистики:  , которая имеет распределение Стьюдента с
, которая имеет распределение Стьюдента с  степенями свободы. Если
степенями свободы. Если 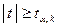 , то проверяемый коэффициент значим.
На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда.Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка
, то проверяемый коэффициент значим.
На основании автокорреляционных коэффициентов осуществляется анализ структуры временного ряда.Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только трендовую и случайную компоненты. Если наиболее высоким оказался коэффициент автокорреляции порядка 



