Проведение аналитического выравнивания временного ряда
Так как наибольшее значение коэффициента детерминации 0, 98 имеет уравнение, заданное кубическим полиномом, то в качестве модели можно использовать это уравнение (рис. 3.4).
Рисунок 3.4. Подбор линии тренда
5. Прогнозирование. Используя наилучшую линию тренда (кубический полином) осуществляется прогноз выпуска продукции, который составит в 2011 году 44208 единиц.
Вопросы для самоконтроля 1. Дайте определение модели временного ряда. 2. Перечислите основные элементы временного ряда. 3. Каковы основные цели исследования временных рядов. 4. Как использовать автокорреляционную функцию при анализе структуры временного ряда. 5. Как рассчитывается коэффициент автокорреляции 5–го порядка? 6. Как строится коррелограмма? 7. Запишите общий вид мультипликативной и аддитивной моделей временного ряда. 8. С какой целью проводится анализ структуры сезонных колебаний временного ряда? 9. Какие тесты используются для проверки гипотезы о структурной стабильности временного ряда? 10. В каком случае нарушается структурная стабильность временного ряда? 11. Что такое аналитическое выравнивание временного ряда? 12. Перечислите наиболее распространенные модели, используемые для аналитического выравнивания временного ряда. 13. Что такое линеаризующие преобразования и как они используются в МНК? 14. Как оценивается качество построенной модели? 15. Как осуществляется точечный прогноз? Индивидуальные задания Динамика выпуска продукции некоторого предприятия характеризуется данными, представленными в таблице 3.1 (в каждом варианте объем выпускаемой продукции надо прибавить число 120* Проанализируйте структуру временного ряда, проверьте гипотезу о структурной стабильности ряда, проведите аналитическое выравнивание временного ряда, сделайте прогноз на 2011 год. ТЕМА 4. ЗАВИСИМОСТЬ ПЕРЕМЕННЫХ, ЗАДАННЫХ ВРЕМЕННЫМИ РЯДАМИ Постановка задачи Построить модель зависимости фактора Y от фактора X по данным наблюдений за 22 месяца, предполагая, что на причинно-следственую связь между ними влияет ложная корреляция, вызванная наличием тренда в каждом из временных рядов факторов (см. таблицу 4.1). Сделать прогноз значения Y для X=15.
Таблица 4.1 – Данные наблюдений
Технология вычислений в Excel взаимосвязи двух временных рядов Ввод данных. В ячейку А1 введите название первого столбца — «Месяц», в ячейку В1 — название второго столбца — «Фактор X», в ячейку С1 — «Фактор Y». В ячейки А2, А3, …, А23 введите данные первого столбца исходной таблицы, в ячейки В2, В3, …, В23 — второго столбца, в ячейки С2, С3, …, С23 – третьего. Переименуйте рабочий лист в «Предварительный анализ рядов». Сохраните рабочую книгу под названием «Зависимость переменных, заданных временными рядами». Предварительный анализ временных рядов каждого наблюдаемого фактора для выявления их структуры и устранения сезонных (циклических) колебаний по их автокореляционным функциям. Построение модели Y=f(X) зависимости фактора Y от фактора X требует устранения сезонности во временных рядах и влияния фактора времени на каждую переменную в модели. Установите порядок наибольшего коэффициента автокорреляции. Для этого выполните действия, описанные в пункте 2.1.2 технологии темы 3, для фактора X в ячейках Е1: F8, а затем для фактора Y в ячейках H1: I8. Если порядок наибольшего коэффициента автокорреляции равен 1, то сезонность отсутствует. Если же временные ряды содержат сезонную компоненту, то ее влияние исключается следующим образом: для каждого уровня находится сезонная составляющая методом скользящей средней, которая вычитается в случае аддитивной модели из наблюдаемых значений или, в случае мультипликативной модели, наблюдаемые значения делятся на сезонную компоненту (см. [8]). Полученные временные ряды факторов X, Y должны содержать только трендовую и случайную компоненты. Устранение влияния фактора времени на каждую переменную в модели методом отклонений от тренда (МОТ). Постройте регрессионную модель зависимости фактора X от времени. Для этого выполните следующие действия. В ячейку А26 введите «Модель временного ряда X». В меню Сервис выберите дополнение Анализ данных укажите Регрессия. Нажмите кнопку ОК. Установите следующим образом значения параметров: · Входной интервал Y — введите ссылки на ячейки В1: В23; · Входной интервал X — введите ссылки на ячейки А1: А23; · Метки — установите флажок; · Уровень надежности — установите флажок; · Константа ноль — не активизируйте; · Параметры вывода — установите флажок на Выходной интервал, поставьте курсор в поле напротив и активизируйте ячейку А27; · Остатки — установите флажок; · Стандартизированные остатки — оставьте пустым; · График остатков — оставьте пустым; · График подбора — оставьте пустым; · График нормальной вероятности — оставьте пустым. Нажмите ОК. Аналогично постройте регрессионную модель зависимости фактора Y от времени в ячейке К26. Остатки каждой модели (отклонения от трендов) проверьте на автокорреляцию. В ячейку С50 введите Остатки по X, в М50 – Остатки по Y (для конкретизации при дальнейшем использовании). Найдите коэффициенты автокорреляции первого порядка. В ячейке С74 введите формулу =КОРРЕЛ(B2: B22; B3: B23). В ячейке M74 введите формулу =КОРРЕЛ(С2: С22; С3: С23). В ячейки B74 и L74 введите Коэф. автокорреляции. Для проверки на значимость коэффициентов автокорреляции выполните следующие действия: · в ячейки В75 и L75 введите tнаблX и tнаблY, соответственно, · в ячейку С75 введите формулу =С74*КОРЕНЬ((22-2)/(1-С74^2)), · в ячейку М75 введите формулу = M74*КОРЕНЬ((22-2)/(1- M74^2)), · в ячейки В76 и L76 введите tкр, · в ячейку С76 и М76 введите формулу =СТЬЮДРАСПОБР(0, 05; 22-2). Сравните наблюдаемое и критическое значения статистик. Если имеется автокорреляция остатков по любой из них, то она устраняется.
|

 ;
– гиперболическая
;
– гиперболическая  ;
– экспоненциальная
;
– экспоненциальная  ;
– степенная
;
– степенная  ;
– полиномы второго и более высоких порядков
;
– полиномы второго и более высоких порядков  .
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время, а в качестве зависимой переменной – фактические уровни временного ряда yt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Известно несколько способов определения типа тенденции. К наиболее распространенным относятся: качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики, коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации
.
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время, а в качестве зависимой переменной – фактические уровни временного ряда yt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Известно несколько способов определения типа тенденции. К наиболее распространенным относятся: качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики, коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации  , значимость которого оценивается по критерию Фишера, и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
При наличии неявной нелинейной тенденции следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, с тем, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, или ускорения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов. В случае если уравнение тренда выбрано неверно при больших значениях выборки, результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибки спецификации.
, значимость которого оценивается по критерию Фишера, и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
При наличии неявной нелинейной тенденции следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, с тем, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, или ускорения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов. В случае если уравнение тренда выбрано неверно при больших значениях выборки, результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибки спецификации.

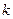 , где
, где 


