Устранение влияния фактора времени на каждую переменную в модели методом отклонений от тренда (МОТ)
Метод отклонений от тренда предполагает построение регрессионной модели отклонений (наблюдаемых значений от трендовых) исследуемых факторов. Для парной регрессии, например, проводят аналитическое выравнивание временных рядов изучаемых показателей, рассчитывая параметры модели  и и  по временным данным. Затем проводят расчет отклонений от трендов: по временным данным. Затем проводят расчет отклонений от трендов:  и и  . Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда. . Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда.
| Анализ регрессионной модели зависимости факторов X и Y от времени на автокорреляцию. Проанализируем остатки временного ряда фактора Х, полученного на листе «Предварительный анализ рядов», на наличие автокорреляции (см. таблицу 4.4).
Для проверки гипотезы о наличии автокорреляции остатков используется кроме статистики Дарбина-Уотсона (см. тему 1) на больших выборках выборочный коэффициент автокорреляции первого порядка, так как DW  . .
|
Таблица 4.4 – Анализ коэффициент автокорреляции первого порядка фактора Х
| Коэф. автокор. x
| 0, 74587667
| | tнабл
| 5, 007869141
| | tкр
| 2, 085963441
| Так как коэффициент автокорреляции первого порядка значим (tнабл > tкр), то автокорреляция присутствует.
Для фактора Y автокорреляция отсутствует (см. таблицу 4.5).
Таблица 4.5 – Анализ коэффициент автокорреляции первого порядка фактора Y
| Коэф. автокор. y
| 0, 422598
| | tнабл
| 2, 085267
| | tкр
| 2, 085963
|
Устранение автокорреляции остатков во временном ряде X(t). Поскольку во временном ряду фактора Х присутствует автокорреляция, то модель этого ряда нельзя использовать в дальнейших исследованиях. Устраним автокорреляцию.
Для устранения автокорреляции можно воспользоваться обобщенным методом наименьших квадратов (ОМНК). Для применения ОМНК необходимо специфицировать модель автокорреляции регрессионных остатков. Обычно в качестве такой модели используется авторегрессионный процесс первого порядка AR (1). Для простоты изложения ограничимся случаем парной регрессии.
Пусть исходное уравнение регрессии   содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрессионной схеме первого порядка содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрессионной схеме первого порядка  , где , где 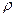 - коэффициент авторегрессии, а - коэффициент авторегрессии, а  - случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как - случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как 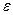 определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина 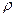 есть коэффициент корреляции между двумя соседними ошибками. Пусть есть коэффициент корреляции между двумя соседними ошибками. Пусть 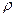 известно.
Обозначим известно.
Обозначим 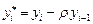 , ,  , , 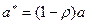 .
Это преобразование и называется авторегрессионым преобразованием первого порядка AR(1) или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнение принимает вид .
Это преобразование и называется авторегрессионым преобразованием первого порядка AR(1) или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнение принимает вид
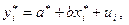 где
где  Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина 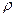 неизвестна. Наиболее простой способ оценить неизвестна. Наиболее простой способ оценить 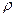 – применить обычный МНК к регрессионному уравнению – применить обычный МНК к регрессионному уравнению  . Коэффициент . Коэффициент  можно также приближенно оценить, используя статистику Дарбина-Уотсона: можно также приближенно оценить, используя статистику Дарбина-Уотсона:  . .
|
На листе «Устранение автокорреляции по Х» получена модель  (см. таблицу 4.6), в которой свободный член не значим (см. тему 1). Поэтому модель была уточнена (см. таблицу 4.7). (см. таблицу 4.6), в которой свободный член не значим (см. тему 1). Поэтому модель была уточнена (см. таблицу 4.7).
Таблица 4.6 – Результаты расчета параметров модели случайной составляющей ряда фактора Х
|
| Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| | Y-пересечение
| -0, 025204468
| 0, 044994
| -0, 56018
| 0, 581902
| | Остатки по Х
| 0, 746565989
| 0, 152951
| 4, 881067
| 0, 000104
| Таблица 4.7 – Результаты расчета параметров уточненной модели случайной составляющей ряда фактора Х
|
| Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| | Y-пересечение
|
| #Н/Д
| #Н/Д
| #Н/Д
| | Остатки по Х
| 0, 742320946
| 0, 15012
| 4, 94485
| 7, 8E-05
|
Из таблицы 4.7 находим значение параметра 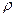 =0, 7423. Используя авторегрессионные преобразования первого порядка AR(1), пересчитаны значения независимой переменной t* и зависимой переменной X* (см. таблицу 4.8) и по данным значениям построена модель Х*= 2, 17+0, 19t* (см. таблицу 4.9), в которой отсутствует автокорреляция остатков (см. таблицу 4.10). В дальнейшем будем использовать ее при построении модели методом отклонения от трендов. =0, 7423. Используя авторегрессионные преобразования первого порядка AR(1), пересчитаны значения независимой переменной t* и зависимой переменной X* (см. таблицу 4.8) и по данным значениям построена модель Х*= 2, 17+0, 19t* (см. таблицу 4.9), в которой отсутствует автокорреляция остатков (см. таблицу 4.10). В дальнейшем будем использовать ее при построении модели методом отклонения от трендов.
.
Таблица 4.8 – Преобразованные значения переменных Х* и t*
| X*
| t*
| | 2, 383364
| 1, 257679
| | 2, 312414
| 1, 515358
| | 2, 528591
| 1, 773037
| | 2, 341262
| 2, 030716
| | 2, 496378
| 2, 288395
| | 2, 585784
| 2, 546074
| | 2, 684393
| 2, 803753
| | 3, 038659
| 3, 061432
| | 3, 033941
| 3, 319111
| | 3, 103147
| 3, 576791
| | 3, 124623
| 3, 83447
| | 3, 038062
| 4, 092149
| | 2, 965272
| 4, 349828
| | 3, 197425
| 4, 607507
| | 3, 187072
| 4, 865186
| | 3, 20665
| 5, 122865
| | 3, 603787
| 5, 380544
| | 2, 75743
| 5, 638223
| | 3, 139321
| 5, 895902
| | 3, 241824
| 6, 153581
| | 3, 42755
| 6, 41126
|
Таблица 4.9 – Результаты расчета параметров модели Х*= f(t*)
|
| Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| | Y-пересечение
| 2, 176939
| 0, 119167
| 18, 26789
| 1, 64E-13
| | t*
| 0, 19474
| 0, 028786
| 6, 765109
| 1, 84E-06
|
Таблица 4.10 – Анализ коэффициент автокорреляции первого порядка фактора Х*
| Коэф автокорр
| 0, 168727
| | tнабл
| 0, 765545
| | tкр
| 2, 085963
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
|
Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются:
• лаконичность...
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
Понятие и структура педагогической техники Педагогическая техника представляет собой важнейший инструмент педагогической технологии, поскольку обеспечивает учителю и воспитателю возможность добиться гармонии между содержанием профессиональной деятельности и ее внешним проявлением...
|
|

 и
и  по временным данным. Затем проводят расчет отклонений от трендов:
по временным данным. Затем проводят расчет отклонений от трендов:  и
и  . Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда.
. Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда.
 .
.

 содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрессионной схеме первого порядка
содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрессионной схеме первого порядка  , где
, где 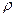 - коэффициент авторегрессии, а
- коэффициент авторегрессии, а  - случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как
- случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как 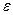 определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина
определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина 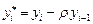 ,
,  ,
, 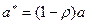 .
Это преобразование и называется авторегрессионым преобразованием первого порядка AR(1) или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнение принимает вид
.
Это преобразование и называется авторегрессионым преобразованием первого порядка AR(1) или преобразованием Бокса-Дженкинса.
Тогда преобразованное уравнение принимает вид
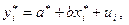 где
где  Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина
Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина  можно также приближенно оценить, используя статистику Дарбина-Уотсона:
можно также приближенно оценить, используя статистику Дарбина-Уотсона:  .
.



