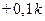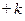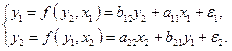Построение регрессионной модели по отклонениям от трендов
Исходные данные (см. таблицу 4.11) для построения модели по отклонениям и ее параметры (см. таблицу 4.12) представлены на листе «Модель по отклонениям».
Таблица 4.11 – Отклонения факторов
Параметры модели Δ Y=f(Δ Х*) представлены в таблице 4.12.
Таблица 4.12 – Результаты расчета параметров модели Δ Y=f(Δ Х*)
Проверка статистической значимости коэффициентов модели (см. тему 1) показывает, что модель требует уточнения. Параметры уточненной модели Δ Y=f(Δ Х*) представлены в таблице 4.13. Таблица 4.13 – Результаты расчета параметров уточненной модели Δ Y=f(Δ Х*)
В модели Δ Y=0, 61Δ Х* автокорреляция отсутствует (см. таблицу 4.14).
Таблица 4.14 – Анализ коэффициент автокорреляции первого порядка
Прогнозирование. Из уравнения модели Х= 0, 19t+8, 6 для Х=15 находится значение t=33, 5. Используя авторегрессионое преобразование первого порядка AR(1)
Таблица 4.15 – Вычисление прогнозного значения
в ячейку А1 Прогноз для Х=15; в ячейку А2 Модель временного ряда X(t); в ячейку D2 Модель временного ряда Y(t); скопируйте: в ячейку А3 ячейки А42: B44 листа Предварительный анализ рядов; в ячейку D3 ячейки K42: L44 листа Предварительный анализ рядов; введите в ячейку А7 Модель временного ряда X*(t*); скопируйте в ячейку А8 ячейки F79: G81 листа Устранение автокорреляции по Х; введите в ячейку А12 Модель авторегрессии временного ряда X(t); скопируйте в ячейку А13 ячейки А40: В42 листа Устранение автокорреляции по Х; введите в ячейку А17 Модель по отклонениям; скопируйте в ячейку А18 ячейки А88: В90 листа Модель по отклонениям; в ячейку B2 ячейки Н88: Н108 листа Устранение автокорреляции по Х; в ячейку С2 ячейки М52: М72 листа Предварительный анализ рядов. Ячейки А22: В31 заполните согласно рисунку 4.3.
Рисунок 4.3 – Вычисление прогноза
Вопросы для самопроверки 1. Что такое ложная корреляция? 2. Изложите суть метода отклонений от тренда. 3. В каком случае используется ОМНК? 4. Перечислите основные этапы ОМНК. 5. Как осуществляется прогнозирование
ТЕМА 5. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ Постановка задачи Имеются данные годового потребления свинины на единицу населения, представленные в таблице 5.1. Таблица 5.1 – Данные наблюдений
Построить линейную структурную модель вида
Для решения этой задачи необходимо: 1. По виду модели (1) определить количество эндогенных, экзогенных переменных в каждом уравнении системы и сделать вывод о ее идентифицируемости. 2. Используя КМНК, оценить по выборочным данным, представленным в таблице 1, коэффициенты приведенной формы модели:
2.1. Методом МНК найдите уравнения регрессий из (2) используя тему 2. 2.2. По найденным приведенным коэффициентам рассчитать структурные коэффициенты, используя правило: Записать структурные уравнения модели (1). Технология вычислений в Excel для модели системы одновременных уравнений 1. Подсчитайте число эндогенных переменных в каждом уравнении системы: – в первом уравнении две (H1=2) эндогенные переменные: – во втором уравнении тоже две (H2=2) эндогенные переменные: Подсчитайте отсутствующие экзогенные переменные в системе: – в первом уравнении одна (D1=1) переменная – во втором уравнении тоже одна (D2=1) переменная Проверьте условие идентифицируемости для каждого уравнения системы: – для первого уравнения D1+1=H1, т. е. 1+1=2, значит, условие выполняется; – для второго уравнения D2+1=H2 , т. е. 1+1=2, значит, условие выполняется; Следовательно, оба уравнения точно идентифицируемы. Поэтому система точно идентифицируема. 2. Постройте уравнения приведенной формы (2), воспользовавшись множественной регрессией (см. тема 2, параметризация) для переменных, выраженных в отклонениях от среднего уровня (т. е. вместо x используйте x-xср, вместо y используйте y-yср.
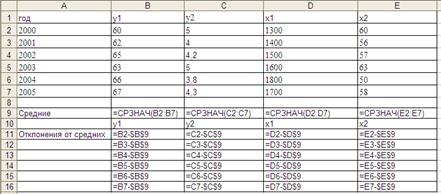
Рисунок 5.1 – Отклонения исходных данных от их средних значений
Рисунок 5.2 – Итоги параметризации уравнений приведенной формы 3. Составьте матрицу системы приведенных уравнений из коэффициентов при переменных x1, x2 копированием соответствующих чисел (см. рис. 5.3).
Рисунок 5.3 – Матрица системы Найдите структурные коэффициенты, используя формулы, приведенные на рисунке 5.4.
Рисунок 5.4 – Формулы расчета структурных коэффициентов по приведенным 4. Запишите уравнения системы в структурной форме.
Анализ модели
1. Так как условия идентифицируемости выполняются для каждого уравнения системы: – для первого уравнения D1+1=H1, т. е. 1+1=2, значит, условие выполняется; – для второго уравнения D2+1=H2 , т. е. 1+1=2, значит, условие выполняется, поэтому система точно идентифицируема. 2. Для построения системы уравнений найдем отклонения от средних, которые будем использовать в качестве новых переменных (названия сохраняются) (см. рис. 5.5).
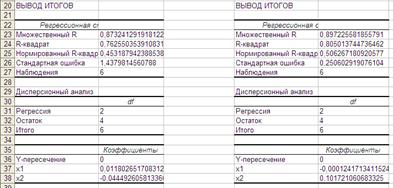
Рисунок 5.5 – Значения отклонений от средних По результатам параметризации (см. рисунки 5.6 и 5.7) имеем следующие уравнения приведенной формы y1= 0, 02 x1 +0.5 x2, y2= 0, 09 x1 – 0, 0004 x2
Рисунок 5.6 – Оценка параметров первого структурного уравнения системы
Рисунок 5.7 – Оценка параметров второго структурного уравнения системы По матрице системы приведенных уравнений из коэффициентов при переменных x1, x2 найдены структурные коэффициенты (см рис. 5.8).
Рисунок 5.8 – Параметры структурного уравнения.
Следовательно, уравнения структурной системы имеют вид y1 = -0.44 y2 +0.012 x1, y2 = 0.1 x2 -0.0105 y1.
Вопросы для самопроверки 1. Каковы основные причины использования систем одновременных уравнений? 2. В чем состоит основное различие между структурной и приведенной формами? 3. Почему не применим МНК для оценки структурных коэффициентов модели? 4. Для оценки каких систем возможно применение МНК? 5. Объясните понятия «экзогенных и эндогенных переменных». 6. Объясните понятия «сверхидентифицируемая система». 7. Сформулируйте необходимое условие идентификации. 8. Сформулируйте достаточное условие идентификации. 9. В чем состоит суть двухшагового метода наименьших квадратов (ДМНК)? 10. Сформулируйте этапы косвенного метода наименьших квадратов. 11. Существует ли единый критерий для оценки общего качества всей системы одновременных уравнений в целом? 12. Приведите модель «спрос – предложение». 13. Какой метод оценок параметров целесообразен для точно идентифицируемого уравнения? 14. Запишите систему рекурсивных уравнений.
Индивидуальные задания Имеются данные годового потребления свинины на единицу населения, представленные в таблице ( Таблица 1 Данные к индивидуальным заданиям (к – номер в журнале)
Построить линейную структурную модель вида
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ 1. Аистов, А. В. Эконометрика шаг за шагом: учеб. пособие для вузов / А. В. Аистов, А. Г. Максимов. — М: ГУ ВШЭ, 2006. — 177 с. 2. Айвазян, С. А. Прикладная статистика и основы эконометрики: учеб. для вузов / С. А. Айвазян, В. С. Мхитрян. — М.: ЮНИТИ, 1998. — 1022 с. 3. Айвазян, С. А. Прикладная статистика. Исследование зависимостей / С. А. Айвазян, И.С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1985. 4. Айвазян, С. А. Прикладная статистика. Основы моделирования и первичная обработка данных / С.А. Айвазян, И.С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. 5. Алексеенко, В. Б. Математические методы исследования экономических систем: учеб. пособие для вузов / Б. В. Алексеенко, В. В. Красавина. — М.: изд-во РУДН, 2005. — 154 с. 6. Бородич, С. А. Эконометрика: учеб. пособие для вузов / С. А. Бородич. — Мн.: Новое знание, 2001. — 408 с. 7. Грубер, Й. Эконометрия. Т. 2: Эконометрические прогнозные и оптимизационные модели: учеб. пособие / Й. Грубер. — Киев: Нiчлава, 1999. — 308 с. 8. Доугерти, К.Введение в эконометрику: учеб. пособие для вузов / К. Доугерти; пер. с англ. под ред. О. О. Замкова. — М.: ИНФРА-М, 1997. — 402 с. 9. Елисеева, И.И. Эконометрика: учебник / И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др.; под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 576 с.: ил. 10. Карминский, А. М. Рейтинги в экономике: методология и практика: учеб. пособие / А. М. Карминский [и др.]; под ред. А. М. Карминского. — М.: Финансы и статистика, 2005. — 240 с. 11. Красс, М. С. Математические методы и модели для магистрантов и экономики: учеб. пособие для вузов / М. С. Красс, Б. П. Чупрынов. — СПб.: Питер, 2006. — 496 с. 12. Калмыкова, Т. Ф. Анализ взаимосвязи экономических показателей: учеб.-метод. пособие / Т. Ф. Калмыкова, Т. М. Моисеева. — Гомель: БТЭУ, 2006. — 52 с. 13. Магнус, Я. Р. Эконометрика. Начальный курс: учеб. пособие / Я. Р. Магнус [и др.]. — М.: Дело, 1997. — 248 с. 14. Маленво, Э. Статистические методы эконометрии / Э. Маленво. — М.: Статистика, 1976. 15. Мардас, А. Н. Эконометрика: учеб. пособие для вузов / А. Н. Мардас. — СПб.: Питер, 2001. — 144 с. 16. Марченко, Л. Н. Теория вероятностей и математическая статистика: [практическое пособие по выполнению лабораторных работ с использованием MS Excel для студентов экономических специальностей] / Л. Н. Марченко, Л. П. Авдашкова; Мин-во образов. РБ, Гомельский государственный университет им. Ф. Скорины. – Гомель: УО «ГГУ им. Ф. Скорины», 2007. – 275 с. 17. Нименья, И. Н.Эконометрика: учеб. пособие / И. Н. Нименья. — СПб.: Нева, 2004. — 224 с. 18. Новак, Э. Введение в методы эконометрики: сборник задач / Э. Новак; пер. с польск. под ред. И. И. Елисеевой. — М.: Финансы и статистика, 2006. — 248 с. 19. Переяслова, И. Г. Статистика: учеб. пособие для вузов / И. Г. Переяслова, Е. Б. Колбачев, О. Г. Переяслова. — Ростов н/Д.: Феникс, 2003. — 288 с. 20. Переяслова, И. Г. Основы статистики: учеб пособие для вузов / И. Г. Переяслова, Е. Б. Колбачев. — Ростов н/Д.: Феникс, 1999. — 320 с. 21. Шелобаев, С. И. Математические методы и модели в экономике, финансах, бизнесе: учеб. пособие для вузов / С. И. Шелобаев. — М.: ЮНИТИ-ДАНА, 2000. — 367 с. 22. Экономико-математические методы и прикладные модели: учеб. пособие для вузов / В. В. Федосеева [и др.]; под ред. В. В. Федосеева. — М.: ЮНИТИ-ДАНА, 2005. — 304 с.
Учебное издание
|

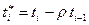 при
при 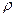 =0, 746, ti =33, 5, ti-1 =32, 5 находится t*=9, 24. По модели X*=0, 19t*+2, 14 вычисляется Х* модельное=3, 94. Для нахождения Х*набл используется авторегрессионное преобразование первого порядка AR(1)
=0, 746, ti =33, 5, ti-1 =32, 5 находится t*=9, 24. По модели X*=0, 19t*+2, 14 вычисляется Х* модельное=3, 94. Для нахождения Х*набл используется авторегрессионное преобразование первого порядка AR(1)  , где
, где 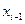 рассчитывается по модели Х= 0, 19t+8, 6 при t=32.5,
рассчитывается по модели Х= 0, 19t+8, 6 при t=32.5, 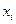 =15 из условия. Отклонение по фактору Х определяется как разность между наблюдаемым и модельным значениями, Δ x*= Х*набл – Х*модельное=0, 0077. Используя модель Δ Y=0, 61Δ Х*, находится Δ Y=7, 62. По модели Y=5, 22+0, 07t при t=33, 5 находится прогнозируемое значение Y=7, 62. С учетом исключения трендов прогнозируемое значение Y = 7, 62+0, 0047= 7, 629.
=15 из условия. Отклонение по фактору Х определяется как разность между наблюдаемым и модельным значениями, Δ x*= Х*набл – Х*модельное=0, 0077. Используя модель Δ Y=0, 61Δ Х*, находится Δ Y=7, 62. По модели Y=5, 22+0, 07t при t=33, 5 находится прогнозируемое значение Y=7, 62. С учетом исключения трендов прогнозируемое значение Y = 7, 62+0, 0047= 7, 629.
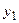 )
)
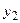 )
)
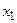 )
)
 )
)
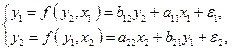 (1)
(1)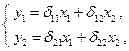 (2)
(2) (3)
(3)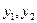 ;
;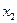 ;
;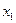 .
.


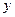 рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов  :
:
 – система рекурсивных уравнений – когда зависимая переменная
– система рекурсивных уравнений – когда зависимая переменная 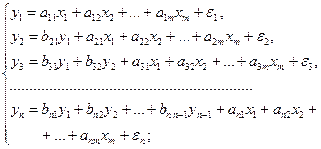 – система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:
– система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:
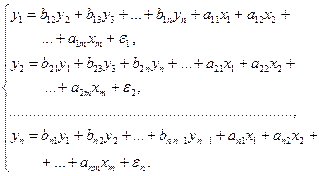 Такая система уравнений называется структурной формой модели.
– приведенная форма уравнений, если определенасхема вычисления эндогенных переменных, т. е.
Такая система уравнений называется структурной формой модели.
– приведенная форма уравнений, если определенасхема вычисления эндогенных переменных, т. е.
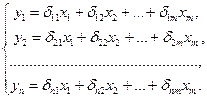 Непосредственное применение МНК для параметризации каждого уравнения системы приводит к получению смещенных и несостоятельных оценок. Обычно это связано с коррелированностью объясняющих переменных со случайными членами. Изменение формы уравнения (например, введением инструментальных переменных и приведением системы к приведенной форме) позволяет устранить коррелированность, но приводит к проблеме идентификации, под которой понимается возможность численной оценки параметров структурных уравнений по оценкам коэффициентов приведенных уравнений
Исходную систему уравнений называют идентифицированной, (точно определенной), если по коэффициентам приведенных уравнений можно однозначно определить значения коэффициентов структурных уравнений.
Исходную систему уравнений называют неидентифицируемой, (недоопределенной), если по коэффициентам приведенных уравнений можно получить несколько вариантов значений коэффициентов структурных уравнений.
Исходную систему уравнений называют сверхидентифицируемой, (переопределенной), если по коэффициентам приведенных уравнений невозможно определить значения коэффициентов структурных уравнений.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо.
Необходимое условие идентификации – выполнение счетного правила:
Непосредственное применение МНК для параметризации каждого уравнения системы приводит к получению смещенных и несостоятельных оценок. Обычно это связано с коррелированностью объясняющих переменных со случайными членами. Изменение формы уравнения (например, введением инструментальных переменных и приведением системы к приведенной форме) позволяет устранить коррелированность, но приводит к проблеме идентификации, под которой понимается возможность численной оценки параметров структурных уравнений по оценкам коэффициентов приведенных уравнений
Исходную систему уравнений называют идентифицированной, (точно определенной), если по коэффициентам приведенных уравнений можно однозначно определить значения коэффициентов структурных уравнений.
Исходную систему уравнений называют неидентифицируемой, (недоопределенной), если по коэффициентам приведенных уравнений можно получить несколько вариантов значений коэффициентов структурных уравнений.
Исходную систему уравнений называют сверхидентифицируемой, (переопределенной), если по коэффициентам приведенных уравнений невозможно определить значения коэффициентов структурных уравнений.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо.
Необходимое условие идентификации – выполнение счетного правила:
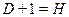 – уравнение идентифицируемо;
– уравнение идентифицируемо;
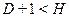 – уравнение неидентифицируемо;
– уравнение неидентифицируемо;
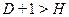 – уравнение сверхидентифицируемо;
где
– уравнение сверхидентифицируемо;
где  – число эндогенных переменных в уравнении,
– число эндогенных переменных в уравнении,
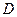 – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для параметризации идентифицируемого уравнения применяется косвенный метод наименьших квадратов, в то время как сверхидентифицированное требует двухшагового метода наименьших квадратов.
Косвенный МНК состоит в следующем:
– составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК по исходным данным;
– путем алгебраических преобразований полученной системы уравнений переходят к уравнениям в структурной форме модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
– составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК по исходным данным;
– выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;
обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения..
– число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для параметризации идентифицируемого уравнения применяется косвенный метод наименьших квадратов, в то время как сверхидентифицированное требует двухшагового метода наименьших квадратов.
Косвенный МНК состоит в следующем:
– составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК по исходным данным;
– путем алгебраических преобразований полученной системы уравнений переходят к уравнениям в структурной форме модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
– составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК по исходным данным;
– выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;
обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения..




 – номер студента в журнале).
– номер студента в журнале).