| Корреляционным полем называется множество точек на плоскости с координатами (xi, yi), i =1, 2, …, n, n – объем выборки.
|
Вид регрессии визуально определяется по корреляционному полю, которое изображено на листе Регрессияна графике подбора черными точками по данным 20 наблюдений из листа Исходные данные (рис. 1.1)
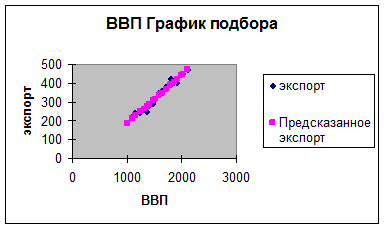
Рисунок 1.1 – Корреляционное поле (график подбора)
Так как точки сгруппированы вдоль прямой (не горизонтальной), то можно предположить, что зависимость экспорта 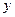 от ВВП x описывается парной линейной регрессионной моделью
от ВВП x описывается парной линейной регрессионной моделью  , где
, где  – неизвестные параметры модели,
– неизвестные параметры модели, 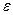 – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.
– случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.
Для характеристики вида связи используется ковариация, рассчитываемая по формуле 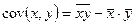 . Если . Если  , то возрастание , то возрастание  приводит к увеличению приводит к увеличению 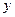 и связь прямая. Если и связь прямая. Если  , то возрастание , то возрастание  приводит к уменьшению приводит к уменьшению 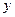 и связь обратная. Если и связь обратная. Если  , то экономические показатели не связаны.
Тесноту связи изучаемых экономических показателей для линейной регрессии оценивает коэффициент парной корреляции , то экономические показатели не связаны.
Тесноту связи изучаемых экономических показателей для линейной регрессии оценивает коэффициент парной корреляции   : :  .
Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью .
Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью  –статистики: –статистики:  . Величина . Величина  имеет распределение Стьюдента с имеет распределение Стьюдента с  степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если |tнабл| степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если |tнабл|  , то коэффициент корреляции значим ( , то коэффициент корреляции значим ( = t кр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таб. 1.2).
Таблица 1.2 – Шкала Чеддока = t кр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таб. 1.2).
Таблица 1.2 – Шкала Чеддока
| Теснота связи
| Значение коэффициента корреляции
при наличии
| | прямой связи
| обратной связи
| | Слабая
| 0, 1–0, 3
| (-0, 1)–(-0, 3)
| | Умеренная
| 0, 3–0, 5
| (-0, 3)–(-0, 5)
| | Заметная
| 0, 5–0, 7
| (-0, 5)–(-0, 7)
| | Высокая
| 0, 7–0, 9
| (-0, 7)–(-0, 9)
| | Весьма высокая
| 0, 9–0, 99
| (-0, 9)–(-0, 99)
|
|
В Excel с помощью пакета «Анализ данных» на листе «Исходныеданные» получены ковариационная и корреляционная матрицы (таблицы 1.3 и 1.4):
Таблица 1.3 – Ковариационная матрица
| ковариация
|
|
| ВВП
| экспорт
|
| ВВП
| 98568, 75
|
|
| экспорт
| 25558, 75
| 6804, 75
|
Таблица 1.4 – Корреляционная матрица
| корреляция
|
|
| ВВП
| экспорт
|
| ВВП
|
|
|
| экспорт
| 0, 986879
|
|
Ковариация между ВВП и экспортом равна 25558, 75 > 0, поэтому зависимость прямая.
Коэффициент корреляции между ВВП и экспортом равен 0, 986879 > 0, то зависимость прямая и весьма высокая.
Проверим на значимость коэффициент корреляции, так как он найден по выборочной совокупности только из 20 наблюдений, что может привести к неверным выводам о всей генеральной совокупности факторов ВВП и экспорт. На листе «Исходныеданные»получены наблюдаемое и критическое значения t-статистики (таблица 1.5):
Таблица 1.5 – Значимость коэффициента корреляции
| tнабл
| 25, 93168
|
| tкр
| 2, 100922
|
Так как | t набл| = 25, 93168 > t кр = 2, 1, то коэффициент корреляции значим (значительно отличается от нуля).
Исходя из проведенного анализа можно выдвинуть предположение о том, что зависимость экспорта от ВВП описывается линейной регрессионной моделью  , где
, где  – неизвестные параметры модели,
– неизвестные параметры модели, 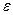 – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений.
– случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений.


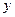 от ВВП x описывается парной линейной регрессионной моделью
от ВВП x описывается парной линейной регрессионной моделью  , где
, где  – неизвестные параметры модели,
– неизвестные параметры модели, 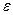 – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.
– случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.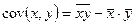 . Если
. Если  , то возрастание
, то возрастание  приводит к увеличению
приводит к увеличению  , то возрастание
, то возрастание  , то экономические показатели не связаны.
Тесноту связи изучаемых экономических показателей для линейной регрессии оценивает коэффициент парной корреляции
, то экономические показатели не связаны.
Тесноту связи изучаемых экономических показателей для линейной регрессии оценивает коэффициент парной корреляции 
 :
:  .
Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью
.
Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью  –статистики:
–статистики:  . Величина
. Величина  степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если |tнабл|
степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если |tнабл|  , то коэффициент корреляции значим (
, то коэффициент корреляции значим ( = t кр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таб. 1.2).
Таблица 1.2 – Шкала Чеддока
= t кр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таб. 1.2).
Таблица 1.2 – Шкала Чеддока
 , где
, где  – неизвестные параметры модели,
– неизвестные параметры модели, 


