Уравнения в безразмерном виде. Понятие о критериях подобия
Теория подобия является одним из наиболее эффективных методов, используемых в математической физике. Смысл законов подобия состоит в том, что они позволяют сворачивать большие многообразия решений в более узкие, подобные группы. Далее будет использован один из подходов к выводу законов подобия – это непосредственное приведение уравнений, начальных и граничных условий задачи к безразмерному виду путем отнесения входящих в них величин к характерным масштабам задачи. Для задач внешнего обтекания все газодинамические переменные отнесем к их значениям в невозмущенном потоке и характерному размеру тела. Тогда в качестве безразмерных переменных используем следующие (см.[14]):
где черточки над функциями относятся к размерным величинам. В качестве примера построим в безразмерных переменных одномерную систему уравнений Навье-Стокса. Учитывая уравнения (8), запишем одномерную систему в следующем виде:
В полной записи:
Упростим второе уравнение системы. Для этого умножим первое уравнение на величину u и вычтем его из преобразованного второго уравнения:
Для упрощения третьего уравнения системы, умножая первое уравнение на величины
Замечание. Все уравнения записаны в размерных переменных. Черточки опущены по умолчанию. В безразмерных переменных преобразованная одномерная система уравнений (11) примет вид:
Задача обтекания геометрически подобных тел, одинаково ориентированных к внешнему потоку, содержит три безразмерных критерия подобия:
Замечание. Одним из важных критериев подобия является число Маха. Число Маха характеризует отношение местной скорости газа к скорости звука и наряду с числом Рейнольдса определяет качественный характер течения. Число Маха имеет и математический смысл, оно определяет вид исследуемого уравнения. Если нестационарные уравнения газовой динамики имеют гиперболический вид, то стационарные уравнения являются гиперболическими в сверхзвуковой области (при М> 1) и эллиптическими – в дозвуковой (при М< 1).
|

 ,
,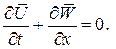
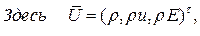
 и вектор потока
и вектор потока 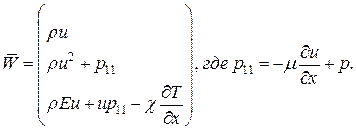


 и
и 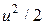 соответственно и по очереди отнимая от третьего уравнения, а затем от оставшейся части третьего уравнения отнимая второе умноженное на величину
соответственно и по очереди отнимая от третьего уравнения, а затем от оставшейся части третьего уравнения отнимая второе умноженное на величину  , получим
, получим . Таким образом, упрощенная одномерная система уравнений Навье – Стокса получается следующая:
. Таким образом, упрощенная одномерная система уравнений Навье – Стокса получается следующая: (11)
(11) (12)
(12)



