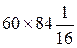Зав.кафедрой ВМ Серба П.В
Редактор
Подписано в печать 22.08.11. Формат 60 × 84 1/16. Бумага офсетная. Усл. печ. л. 13, 2. Уч-изд. л. 12, 2. Тираж 100 экз. Заказ Цена договорная
ФГБОУ ВПО «Челябинский государственный университет» 454001 Челябинск, ул. Братьев Кашириных, 129
Издательство Челябинского государственного университета
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южный федеральный университет» А.Г.Клово, В.В.Семенистый «Разностные методы решения задач прикладной механики» Учебное пособие Декан ЕГФ Куповых Г. В. Зав.кафедрой ВМ Серба П.В. Таганрог 2012
УДК Рецензенты: Канд.физ.-мат.наук, доцент каф. математического анализа ПИ ЮФУ, Безмагорычный В.В.
Клово А.Г., Семенистый В.В. Разностные методы решения задач прикладной механики: Учебное пособие.- Таганрог: Изд-до ЮФУ, 2012.-87с. Учебное пособие написано на основе лекций, читаемых автором на протяжении ряда лет студентам специальности прикладная математика и информатика. В учебном пособии рассматриваются вопросы, связанные с проблемами численного моделирования задач механики сплошной среды. Приведены физико-математические модели и указаны для внешних задач гидроародинамики области их применимости. При разностном решении физических моделей используются наиболее популярные в последние десятилетия численные алгоритмы, В пособии содержится спектральный анализ выбранных разностных моделей. Пособие написано для студентов прикладных математических специальностей, но может быть полезно всем, кто занимается численной механикой.
Ил. 3. Библиогр.: 17 назв.
Печатается по решению редакционно-издательского совета Таганрогского кампуса ЮФУ
ЮФУ, 2013 Семенистый В.В., 2012
Клово А.Г., Семенистый В.В.
Учебное пособие «Разностные методы решения задач прикладной механики»
Ответственный за выпуск Семенистый В.В. Редактор Кочергина Т.Ф. Корректор Селезнева Н.И.
ЛР № 020565 от 23.06.97 г. Подписано к печати Формат Печать офсетная. Бумага офсетная. Усл.п.л.- 1, 8 Уч.-изд. -!, 5 Заказ № Тираж 50 экз.
«С» ----------------------------------------------------------------------------------------------------Издательство Инженерной академии Южного федерального университета ГПС 17А, Таганрог, 28, Некрасовский, 44 Типография Таганрогского кампуса Южного федерального университета ГПС 17А, Таганрог, 28, Энгельса, 1 ОГЛАВЛЕНИЕ Введение… …………………………………………………................. 3 1. Физико – математические модели......................................................... 4 1.1 Система уравнений движения вязкого сжимаемого теплопроводного газа. Простейшие физические процессы...4 1.2 Уравнения в безразмерном виде. Понятие о критериях подобия................................................................................... 15 1.3 Переход к недивергентным формам записи системы уравнений Навье-Стокса.........................................................18 1.4 Расщепление уравнений системы, записанной в недивергентной форме...........................................................25 1.5 Различные упрощенные модели полной системы уравнений Навье – Стокса......................................................................…27 1.6 Краевые условия для задач внешнего обтекания..................39 2. Разностные методы решения уравнений ……………………. 42 2.1 Основные понятия теории разностных схем. 42 2.2 Явные разностные схемы для модельных уравнений........44 2.3 Безусловно устойчивые неявные разностные схемы для модельных уравнений..............................................................47 2.4 Разностные схемы для системы модельных уравнений…....51 2.5 Разностные схемы для системы уравнений газовой динамики, записанной в дивергентной форме.......................59 2.6 Понятие о монотонных разностных схемах...........................64 2.7 Схемы для одномерных уравнений газовой динамики и Навье – Стокса представленные в недивергентной форме...66 2.8Уравнения газовой динамики и Навье-Стокса в комбинированных газодинамических переменных..............76 2.9 Схема с несогласованным стабилизирующим оператором..83 2.10 Схемы для решения стационарных задач.............................86 2.11 Несколько замечаний для многомерных уравнений..........90 3. Заключение.................................................................................. 90
|