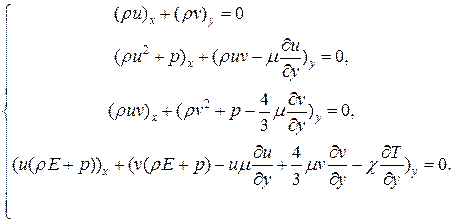Различные упрощенные модели полной системы уравнений Навье-
Стокса В этом разделе будут рассмотрены упрощенные модели системы уравнений Навье-Стокса в дальнейшем, используемые при построении дискретных аналогов. Это линеаризованная система уравнений Навье-Стокса, модель вязкой несжимаемой жидкости, система уравнений пограничного слоя, система уравнений вязкого ударного слоя и параболизованная система уравнений Навье-Стокса.Выбор моделей с одной стороны обусловлен их широкой применимостью при расчетах различных областей течения (см.рис.3), а с другой стороны позволяет значительно сэкономить вычислительные ресурсы. Линеаризованная система уравнений Навье-Стокса. В некоторых задачах механики сплошной среды исследуемые движения и процессы имеют характер малых возмущений некоторых состояний равновесия или основного движения. В аэродинамики, например, при изучении движения различных тонких тел в воздухе в направлении их основного размера, когда угол наклона скорости полета к элементам поверхности тел мал, движение вызывает в основной массе воздуха малые скорости возмущения. В тех случаях, когда допущение о малости искомых функций является приемлемым, в постановке задач можно провести линеаризацию. Пусть известен вектор состояния основного течения Здесь Рассмотрим первое уравнение системы (15): Заменим искомые функции через основное и возмущенное решения, тогда Так как Аналогично преобразовывается второе и третье уравнения системы (15) получаем:
Эта система может быть решена и аналитически. В случае баротропного течения когда,
Здесь
При невязком течении (т.е.
Модель вязкой несжимаемой жидкости Среда называется несжимаемой, если любой ее индивидуальный объем остается постоянным по величине во все время движения. Плотность в частице несжимаемой среды также остается постоянной. Уравнение неразрывности (1) сводится к следующему уравнению: Системы уравнений ламинарного пограничного слоя Один из методов получения упрощенных моделей из полной системы уравнений Навье – Стокса основан на гипотезе о том, что толщина пристеночной области, в которой вязкость и теплопроводность играют существенную роль, а также величина нормальной к направлению потока составляющей скорости в этой области имеют порядок Уравнения и основные понятия теории пограничного слоя были установлены в 1904 г. Л.Прандтлем. Для получения уравнений теории пограничного слоя рассмотрим задачу об обтекании несжимаемой вязкой жидкостью тонкой пластинки, поставленной по направлению набегающего потока.
Рис.1 Пусть L – некоторый характерный размер, например длина пластинки. Обозначим через δ «толщину» пограничного слоя (см.рис.1). По основному допущению примем, что на расстоянии δ по нормали от поверхности пластинки имеется «граница» пограничного слоя. Величина δ или, точнее, отношение Заменяя переменные
Теперь оценим слагаемые первого уравнения движения:
При исследовании пограничного слоя предполагают, что влияние вязких слагаемых сопоставимо с влиянием конвективных слагаемых и слагаемых, связанных с силами давления, то есть по порядку эти слагаемые должны быть одинаковы. Второй член правой части уравнения, по предположению, имеет одинаковый порядок со слагаемыми левой части уравнения, тогда:
Оценим слагаемые второго уравнения движения:
Окончательно получаем следующую систему пограничного слоя:
Уравнения (18) остаются нелинейными. Поперек пограничного слоя давление сохраняется постоянным и определяется значением на границе слоя в основном потоке, следовательно, в первом уравнении член Эта система была предложена Прандтлем и используется только для расчета течения в пограничном слое. Ее нельзя использовать для внешнего течения. Но если 2-е уравнение системы заменить на уравнение:
Система уравнений Прандтля, полученная ранее, представляет собой первое «приближение», точнее приближение, содержащее малый параметр в нулевой степени в асимптотическом разложении решений уравнений Навье-Стокса по малому параметру. При последующих приближениях, содержащих малый параметр в нулевой и первой степени (
Параболизированная система уравнений Навье-Стокса (ПУНС) ПУНС используется при численном исследовании сверхзвуковых течений (особенно стационарных задач) и получается из полной системы уравнений Навье – Стокса после исключения всех 2-х производных (повторных и смешанных), содержащих дифференцирование вдоль потока (см.[7]). ПУНС по точности занимает промежуточное место между уравнениями вязкого ударного слоя и обобщенными уравнениями Прандтля, так как содержит слагаемые старшего порядка малости, чем в уравнении пограничного слоя. В качестве примера рассмотрим также задачу обтекания плоской пластины, но уже однородным потоком вязкого сжимаемого теплопроводного газа.
Рис.2
Выпишем полную стационарную систему уравнений Навье-Стокса, описывающую данное течение, которая в векторной записи равна:
Заменяя элементы тензора вязких напряжений:
Пораболизированная система уравнений Навье-Стокса получается при выбрасывании из уравнений всех повторных производных, содержащих хотя бы одно дифференцирование по
Иллюстрация применимости моделей Для иллюстрации применимости различных упрощенных уравнений рассмотрим задачу обтекания тела конечного размера сверхзвуковым потоком сжимаемого вязкого теплопроводного газа (см.[6]). Задача рассматривается при умеренных числах Маха (не больше 6), так как при М≈ 6 температура газа у поверхности тела может достигать нескольких тысяч градусов, а в такой ситуации для правильного описания течения необходимо рассматривать течение как многокомпонентную химически реагирующую смесь.
Рис.3 На рис. 3 обозначены следующие зоны течения: 1 – Головной скачок уплотнения. 2 – Область слабовязкого течения между ударной волной и пограничным слоем. 3 – Пограничный слой. 4 – Волны разрежения. 5 – Область возвратного течения. 6 – Кормовой скачок. 7 – Висящий пограничный слой. 8 – Хвостовой скачок. 9 – Горло следа. 10 – Ближний след. 11 – Дальний след. Для изучения течения в области 2 справедлива модель уравнений газовой динамики, в области 3 – система уравнений пограничного слоя, в областях 5 и 9
|

 .В течение вносятся малые возмущения:
.В течение вносятся малые возмущения:  ,
,  ,
, 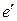 ,
,  .
. . Искомое решение можно представить в виде
. Искомое решение можно представить в виде  В этом случае систему уравнений (15) можно линеаризовать (метод замороженных коэффициентов).
В этом случае систему уравнений (15) можно линеаризовать (метод замороженных коэффициентов).
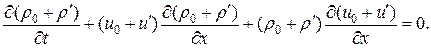
 , то производные от них равны нулю. Получаем линеаризованное уравнение с постоянными коэффициентами:
, то производные от них равны нулю. Получаем линеаризованное уравнение с постоянными коэффициентами: 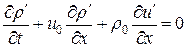 , в котором опущены слагаемые старшего порядка малости.
, в котором опущены слагаемые старшего порядка малости. (17)
(17)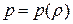 , система (17) упрощается. Опускается уравнение энергии и в уравнении движения пересчитывается производная от давления по формуле:
, система (17) упрощается. Опускается уравнение энергии и в уравнении движения пересчитывается производная от давления по формуле:

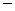 скорость звука. Система (17) преобразуется в следующую:
скорость звука. Система (17) преобразуется в следующую:
 ) дальнейшее упрощение системы приводит к системе уравнений газовой динамики, которую можно записать в операторном виде:
) дальнейшее упрощение системы приводит к системе уравнений газовой динамики, которую можно записать в операторном виде:  где
где  и
и  . Если движение начинается с состояния покоя
. Если движение начинается с состояния покоя  , то мы приходим к уравнению акустики
, то мы приходим к уравнению акустики  .
. , а уравнения движения (2) (в двумерном случае) равны:
, а уравнения движения (2) (в двумерном случае) равны:  и
и 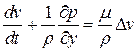 . Здесь вектор скорости
. Здесь вектор скорости  =(
=( . Эта модель используется для вывода следующей
. Эта модель используется для вывода следующей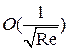 . Сохранение слагаемых в уравнениях Навье – Стокса различного порядка малости
. Сохранение слагаемых в уравнениях Навье – Стокса различного порядка малости  ,
,  и приводит к построению различных приближенных моделей сжимаемого теплопроводного газа.
и приводит к построению различных приближенных моделей сжимаемого теплопроводного газа.
 принимается в качестве малой величины. Воспользуемся преобразованием
принимается в качестве малой величины. Воспользуемся преобразованием  и предположим, что в пограничном слое переменные
и предположим, что в пограничном слое переменные  изменяются в конечных пределах, а интервал изменения переменной y имеет порядок δ (см.[14]). Примем также, что величины U(t)
изменяются в конечных пределах, а интервал изменения переменной y имеет порядок δ (см.[14]). Примем также, что величины U(t)  внутри пограничного слоя и на его границе с основным потоком конечны.
внутри пограничного слоя и на его границе с основным потоком конечны. и используя принятые выше допущения, оценим слагаемые в каждом уравнении модели вязкой несжимаемой жидкости и укажем их порядки. В уравнении неразрывности:
и используя принятые выше допущения, оценим слагаемые в каждом уравнении модели вязкой несжимаемой жидкости и укажем их порядки. В уравнении неразрывности:  . Предполагая, что слагаемые уравнения должны быть одинаковые по порядку, получим оценку для нормальной компоненты скорости:
. Предполагая, что слагаемые уравнения должны быть одинаковые по порядку, получим оценку для нормальной компоненты скорости:
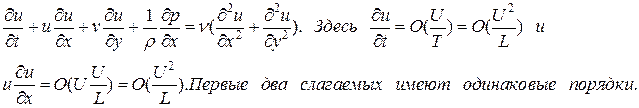 Остальные слагаемые левой части по порядку тоже равны первым:
Остальные слагаемые левой части по порядку тоже равны первым: 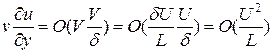 и
и  . Остается оценить вязкие члены уравнения. Получаем
. Остается оценить вязкие члены уравнения. Получаем  и
и  . Сравнивая между собой эти слагаемые, имеем:
. Сравнивая между собой эти слагаемые, имеем:  , т.е. второе слагаемое намного больше первого.
, т.е. второе слагаемое намного больше первого.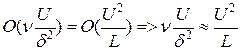 . Получаем оценку на «толщину» пограничного слоя:
. Получаем оценку на «толщину» пограничного слоя:  и малый параметр:
и малый параметр: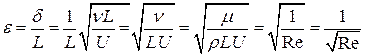 .
.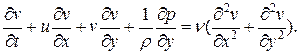 Тогда
Тогда . Остальные члены второго уравнения тоже будут меньшего порядка по сравнению со слагаемыми первого уравнения (проверить самостоятельно), кроме члена с давлением. Остается только слагаемое
. Остальные члены второго уравнения тоже будут меньшего порядка по сравнению со слагаемыми первого уравнения (проверить самостоятельно), кроме члена с давлением. Остается только слагаемое  или
или  .
. (18)
(18) можно считать известным.
можно считать известным. то получаем систему уравнений вязкого ударного слоя, которая уже может быть использована для расчета и внешнего течения.
то получаем систему уравнений вязкого ударного слоя, которая уже может быть использована для расчета и внешнего течения. и
и 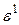 ), получают систему обобщенных уравнений Прандтля и т.д.
), получают систему обобщенных уравнений Прандтля и т.д.
 . Подставляя вектора потоков имеем:
. Подставляя вектора потоков имеем:
 =0
=0 , получаем следующую систему уравнений:
, получаем следующую систему уравнений: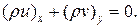
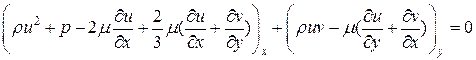
 .
.
 . Получаем
. Получаем