Для модельных уравнений
В качестве промежуточной разностной схемы, которая реализуется так же просто, как явная схема и при определенных физических ограничениях имеет безусловный запас устойчивости, рассмотрим схему бегущего счета(уголок) для уравнения (19): Шаблон, используемый в схеме, позволяет явно находить значения сеточной функции на верхнем временном слое по формуле: Другим примером гибридных разностных схем являются схемы с весами. Для уравнения (20)
При Исследуем условие устойчивости схемы (26). Подставляя вектор гармоники (23), получаем следующее характеристическое уравнение:
С другой стороны, расписывая более подробно разностное уравнение (26) получаем
Преобразуем его к трехточечному виду для решения методом прогонки: В нашем случае прогоночные коэффициенты равны:
Вспомним достаточное условие корректности и устойчивости метода прогонки (условие диагонального преобладания): Получаем следующее неравенство:
Рассматривая только конвективные члены (
Замечание. Чтобы избежать этого ограничения, необходимо аппроксимировать не центральными разностями, а односторонними. Разностная схема с весами для нелинейных уравнений Схемы для нелинейных уравнений строятся аналогично, однако их реализация значительно усложняется. Рассмотрим схему с весами для уравнения (22):
При нелинейной зависимости Мы рассмотрим другой подход, основанный на линеаризации нелинейной системы. Заменим значение
|

 следующего вида:
следующего вида:  .
. . Данная схема будет безусловно устойчивой, так как изначально она неявная. По арифметическим затратам она эквивалентна явной схеме. Недостаток схемы
. Данная схема будет безусловно устойчивой, так как изначально она неявная. По арифметическим затратам она эквивалентна явной схеме. Недостаток схемы  ограничение на параметр
ограничение на параметр  . Если это условие не выполняется, то расчет значительно усложняется.
. Если это условие не выполняется, то расчет значительно усложняется.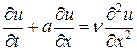 схема с весами следующая:
схема с весами следующая: (26).
(26). – схема явная и если
– схема явная и если  – схема неявная. Порядок аппроксимации схемы:
– схема неявная. Порядок аппроксимации схемы:  . Когда
. Когда  , то
, то  , то есть порядок аппроксимации схемы
, то есть порядок аппроксимации схемы  . При всех остальных значениях
. При всех остальных значениях  – схема первого порядка аппроксимации.
– схема первого порядка аппроксимации.
 или, обозначая
или, обозначая  и
и  , имеем:
, имеем: 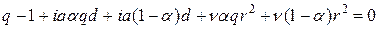 . После преобразования получаем:
. После преобразования получаем: .
.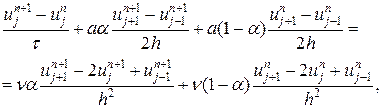
 .
.
 . Одно из неравенств должно быть строгим.
. Одно из неравенств должно быть строгим. .
. ), имеем:
), имеем: Получили, что даже в неявной схеме выполняется условие условной устойчивости.
Получили, что даже в неявной схеме выполняется условие условной устойчивости. .
. для решения уравнения необходимо применять итерационные методы.
для решения уравнения необходимо применять итерационные методы. его разложением по формуле Тейлора до членов второго порядка малости:
его разложением по формуле Тейлора до членов второго порядка малости: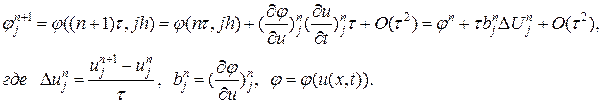 Подставляя
Подставляя  :
: или эквивалентную ей схему в каноническом виде:
или эквивалентную ей схему в каноническом виде: . Ее решение может быть получено скалярной прогонкой. При
. Ее решение может быть получено скалярной прогонкой. При 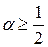 схема безусловно устойчива.
схема безусловно устойчива.


