Разностные схемы для системы модельных уравнений
Среди рассмотренных ранее упрощенных моделей полной системы уравнений Навье-Стокса система уравнений газовой динамики в случае баротропного течения была записана в следующем операторном виде:
где Рассмотрим наиболее используемые разностные схемы для решения этой системы уравнений. Одной из наиболее известных разностных схем решения системы (27) является явная схема Маккормака (см.[16]):
В отличие от разностной схемы для модельного уравнения неизвестной тут является вектор-функция, но порядок аппроксимации и условная устойчивость схемы сохраняется. Найдем условие устойчивости для системы (28). Для этого преобразуем ее в схему с целыми временными шагами. Из первого уравнения системы (28) находим
Исследуем устойчивость схемы (28) для решений вида: Подставляя волновой вектор в последнее уравнение, получим:
Теперь можно выписать характеристическое уравнение для системы (28). Обозначая
Раскрывая определитель, находим корни характеристического уравнения:
После соответствующих преобразований первое уравнение равно: Аналогично для второго уравнения: Предложенная схема не является экономичной из-за ограничений на временной шаг. Можно рассмотреть неявные схемы, которые не обладают этим недостатком. Схема с весами Для системы уравнений (27) теперь рассмотрим разностную схему с весами
имеющую порядок аппроксимации
Схема безусловно устойчива при
Разностную схему с весами можно представить в виде разностного уравнения с матричными коэффициентами решаемого методом векторной прогонки, которая плохо обусловлена при
Рассмотрим теперь аппроксимацию частных производных в уравнениях (27) несимметричными разностными операторами. В случае несимметричных схем аппроксимацию конвективных членов следует согласовывать с аппроксимацией члена с давлением. Например чисто неявная схема (здесь разностный оператор выбирается в зависимости от знака скорости
будет условно устойчива при Для получения безусловно устойчивой схемы необходимо слагаемые, отвечающие градиенту давления, аппроксимировать сопряженным разностным оператором по отношению к конвективным слагаемым, например:
Для получения схем, которые будут реализовываться более просто, то есть либо по схеме бегущего счета, либо как явные схемы, часть слагаемых аппроксимируют на нижнем временном слое. Но все эти схемы становятся условно устойчивыми. Рассмотренные ранее схемы были неэкономичными в смысле того, что реализовывались в одномерном случае векторными прогонками, а в многомерном случае – матричными прогонками, или получались условно устойчивыми. Поэтому предлагается провести расщепление дифференциальных, а, следовательно, и разностных операторов, для получения более экономичных схем. Рассмотрим расщепление по физическим процессам для системы уравнений:
Одним из вариантов реализации схемы расщепления есть следующая схема в дробных шагах:
Рассмотрим более подробно реализацию схемы на дробных шагах, используя для аппроксимации центральные разности. На первом дробном шаге решается следующая система:
Так как матрица На втором дробном шаге решается система:
Из первого уравнения системы выражаем
Последнее уравнение решается методов пятиточечной прогонки. Исследуем устойчивость разностной схемы. Представим вектора решений на различных временных шагах в виде Для первого уравнения системы (29) в случае симметричной аппроксимации получаем следующее характеристическое уравнение:
Аналогично для второго дробного шага получаем
Схема безусловно устойчива. Схемы приближенной факторизации Для получения схем второго порядка аппроксимации можно использовать метод приближенной факторизации. Рассмотрим его на примере схемы с весами для уравнения (27):
или в канонической форме: Используя расщепление матрицы А по физическим процессам, перепишем уравнение в виде:
Факторизация стабилизирующего оператора состоит в следующем:
если
где Данная схема является экономичной и аппроксимирует исходную систему с тем же порядком, что и схема с весами. Реализация схемы на дробных шагах аналогична ранее рассмотренной схемы. Схема безусловно устойчива при
Рассмотренные схемы в дробных шагах и приближенной факторизации можно обобщить и на полную систему уравнений газовой динамики и на систему уравнений Навье-Стокса, не теряя при этом устойчивости схемы и порядка аппроксимации.
|

 , (27)
, (27) .
.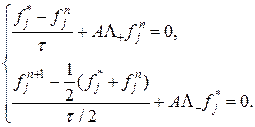 (28)
(28)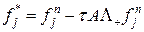 и, подставляя во второе уравнение, имеем:
и, подставляя во второе уравнение, имеем: или
или =
= 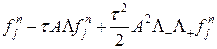 .
. .
.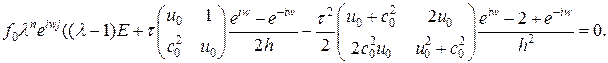
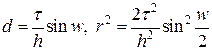 , имеем:
, имеем: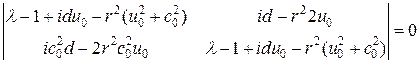 .
.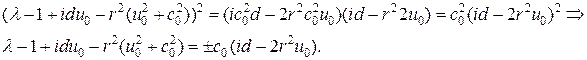
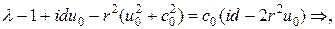
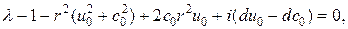
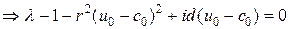 и
и 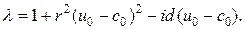
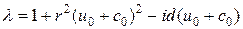 . Тогда
. Тогда 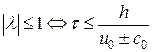 – условие устойчивости. Данная схема условно устойчива.
– условие устойчивости. Данная схема условно устойчива. ,
, Здесь
Здесь 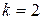 , при
, при  и
и 
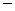 в остальных случаях. Проведем спектральный анализ устойчивости схемы с весами. В этом случае получаем следующее характеристическое уравнение:
в остальных случаях. Проведем спектральный анализ устойчивости схемы с весами. В этом случае получаем следующее характеристическое уравнение: , где
, где  .
.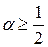 , что следует из вида характеристического уравнения:
, что следует из вида характеристического уравнения: .
.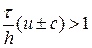 . Таким образом, данная схема является неэкономичной.
. Таким образом, данная схема является неэкономичной. )
)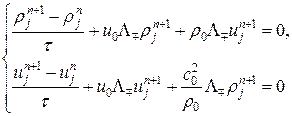
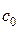 .
.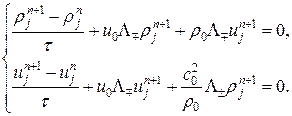
 . Представим матрицу
. Представим матрицу  в виде суммы двух матриц, где
в виде суммы двух матриц, где  . Матрица
. Матрица 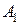 содержит слагаемые, связанные с конвективными членами уравнения, а матрица
содержит слагаемые, связанные с конвективными членами уравнения, а матрица 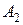 – аналог члена с давлением в уравнении движения и члена вида
– аналог члена с давлением в уравнении движения и члена вида  в уравнении неразрывности. Расщепление матрицы А порождает расщепление дифференциальных операторов на
в уравнении неразрывности. Расщепление матрицы А порождает расщепление дифференциальных операторов на и как следствие
и как следствие  .
.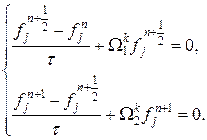 (29)
(29)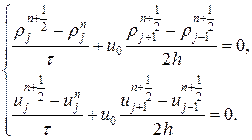
 – диагональная, то уравнения можно решать скалярными прогонками независимо друг от друга, а для
– диагональная, то уравнения можно решать скалярными прогонками независимо друг от друга, а для 
 и подставляем во второе уравнение для нахождения параметра
и подставляем во второе уравнение для нахождения параметра  , т.е.
, т.е.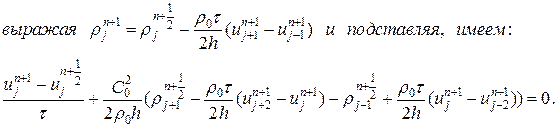
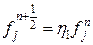 и
и 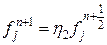 . Тогда
. Тогда 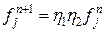 . Оценим значения
. Оценим значения  .
.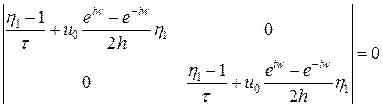 . Раскрывая определитель, имеем
. Раскрывая определитель, имеем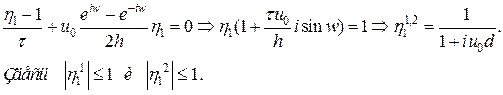
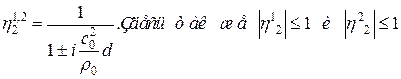 . Все
. Все 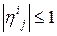 и следовательно их произведение тоже по модулю меньше единицы.
и следовательно их произведение тоже по модулю меньше единицы.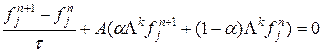
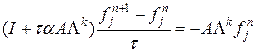 .
.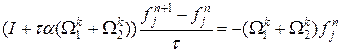 .
.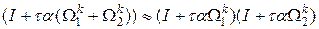 . Тогда схема вида
. Тогда схема вида 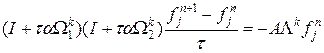 и называется схемой приближенной факторизации. Она может быть реализована в дробных шагах:
и называется схемой приближенной факторизации. Она может быть реализована в дробных шагах: , то
, то
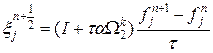 .
.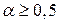 и корни характеристического уравнения в случае симметричной аппроксимации равны:
и корни характеристического уравнения в случае симметричной аппроксимации равны: .
.


