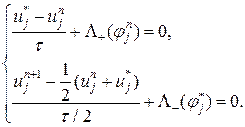Явные разностные схемы для модельных уравнений
Для численного решения уравнения (19) используем следующее явное разностное уравнение
Для устойчивости разностного уравнения корни характеристического уравнения должны по модулю быть не больше единицы. Преобразуя уравнение (24) имеем:
Для того, чтобы схема стала устойчивой, необходимо аппроксимировать оператор
Условие (25) и есть условие устойчивости схемы, называемое условием Куранта-Фридрихса-Леви (CFL). Повысить запас устойчивости первоначальной схемы
Аналогично строятся разностные схемы и для уравнения (20) с вязким слагаемым. Разностная схема:
Рассмотрим несколько явных разностных уравнений второго порядка аппроксимации по времени и по пространству. Это двухшаговые схемы Лакса-Вендрофа и Маккормака типа «предиктор-корректор». Разностная схема Лакса-Вендрофа для уравнения (1) имеет следующий вид:
Здесь Покажем, что схема второго порядка аппроксимации
Преобразуя разностные операторы и заменяя имеющую порядок аппроксимации Схема Лакса-Вендрофа условно устойчива. Условие устойчивости совпадает с условием устойчивости (25). Модификации этой схемы, не требующие введения дробных шагов, предложены Маккормаком. Один из вариантов схемы Маккормака для нелинейного уравнения (21):
Порядок аппроксимации схемы Маккормака Замечания. После линеаризации схема Маккормака в целых шагах совпадает со схемой Лакса-Вендрофа, поэтому порядок аппроксимации у нее такой же, как и у схемы Лакса-Вендрофа. Рассмотренные явные схемы имеют ограничения на временной шаг (условие CFL), что приводит к значительному увеличению расчетного времени. Для получения безусловно устойчивых схем необходимо использовать неявные аппроксимации исходных уравнений.
|

 , аппроксимирующее уравнение (19) с порядком
, аппроксимирующее уравнение (19) с порядком  . Проведем анализ устойчивости, отыскивая решение разностного уравнения в виде гармоники:
. Проведем анализ устойчивости, отыскивая решение разностного уравнения в виде гармоники:  (23). Здесь
(23). Здесь ,
,  .Получим характеристическое уравнение
.Получим характеристическое уравнение  . (24)
. (24)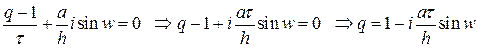 . В результате получаем
. В результате получаем 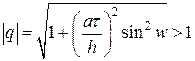 и схема является неустойчивой.
и схема является неустойчивой. , учитывая знак числа
, учитывая знак числа  и используя односторонние разности (схема против потока). Разностная схема
и используя односторонние разности (схема против потока). Разностная схема аппроксимирует уравнение (19) с порядком
аппроксимирует уравнение (19) с порядком  и условно устойчива. Характеристическое уравнение
и условно устойчива. Характеристическое уравнение  и
и если
если  . (25)
. (25)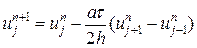 можно и не уменьшая порядка точности. Для этого усредним первое слагаемое в правой части уравнения и рассмотрим следующую схему Лакса:
можно и не уменьшая порядка точности. Для этого усредним первое слагаемое в правой части уравнения и рассмотрим следующую схему Лакса: Схема условно устойчива, но с условной аппроксимацией.
Схема условно устойчива, но с условной аппроксимацией. аппроксимирует (20) с порядком
аппроксимирует (20) с порядком  .
.

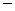 значения сеточной функции на дробном временном шаге.
значения сеточной функции на дробном временном шаге. при выборе шага
при выборе шага  . Из первого уравнения выразим значения сеточной функции на дробном шаге и подставим во второе уравнение. Получим уравнение в целых шагах, эквивалентное исходному.
. Из первого уравнения выразим значения сеточной функции на дробном шаге и подставим во второе уравнение. Получим уравнение в целых шагах, эквивалентное исходному.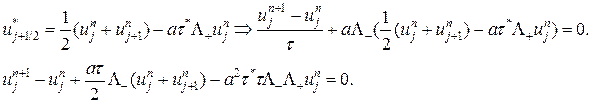
 ,
, .
.