Разностные схемы, записанные в дивергентной форме
Для системы уравнений газовой динамики Рассмотрим систему одномерных уравнений газовой динамики, записанных в декартовых координатах в дивергентной форме:
где Здесь Запишем схему с весами для системы уравнений газовой динамики:
Схема является консервативной и аппроксимирует систему уравнений (30) с порядком При
где
Уравнение (31) линейно относительно вектора
коэффициенты которого вычисляются по формулам:
Здесь используется однородность функции Рассмотрим случай идеального газа. В этом случае уравнение состояния Найдем коэффициенты матрицы Обозначим тогда и
Задание. Найти самостоятельно коэффициенты В итоге получаем следующую матрицу
Исследуем устойчивость схемы (31) для уравнений с замороженными коэффициентами (матрица В постоянная). При решении характеристического уравнения получаем следующие корни (в случае симметричной аппроксимации):
Здесь Параметрическая схема с весами для решения полной системы уравнений Навье-Стокса Изменяется вектор гидродинамического потока. Появляются в системе уравнений производные второго порядка по пространственным переменным. Одномерная дивергентная система уравнений Навье – Стокса записывается в виде
где Для разностного решения системы (32) воспользуемся следующей схемой с весами:
Здесь вектор потока
Изменяя порядок дифференцирования
Для построения канонического вида разностной схемы преобразуем третье слагаемое уравнения.
Замечание. Для аппроксимации производной
Заменяя в схеме (33) значение вектора потока
Полученная схема аппроксимирует систему уравнений (32) с тем же порядком, что и схема (30) и в линейном приближении безусловно устойчива. Вид матриц
|

 ,
,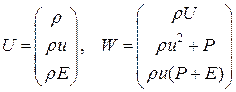 .
.
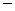 плотность полной энергии и уравнение состояния:
плотность полной энергии и уравнение состояния: 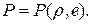
 . (30)
. (30) .
. схема нелинейная относительно верхнего временного слоя и для ее безытерационной реализации линеаризуем вектор
схема нелинейная относительно верхнего временного слоя и для ее безытерационной реализации линеаризуем вектор 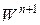 относительно вектора
относительно вектора  . Для этого разложим вектор
. Для этого разложим вектор 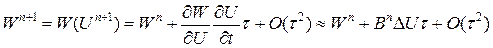 ,
,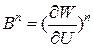
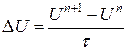 аппроксимация производной
аппроксимация производной 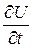 . Заменяя вектор
. Заменяя вектор 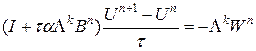 . (31)
. (31)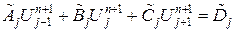
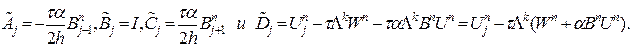
 .
.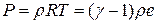 , где
, где 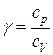 и
и  .
.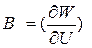 .
.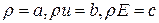 ,
,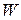 =
= 
 . Для коэффициентов матрицы В имеем:
. Для коэффициентов матрицы В имеем: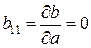 ,
,  ,
,  ,
, ,
, ,
,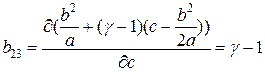 .
.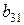 ,
, 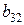 ,
, 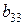 .
.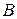 :
: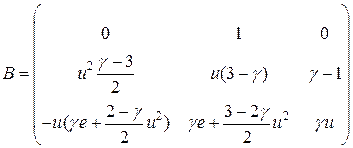 .
. .
. - квадрат скорости звука и
- квадрат скорости звука и  . При
. При 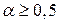 схема безусловно устойчивая.
схема безусловно устойчивая.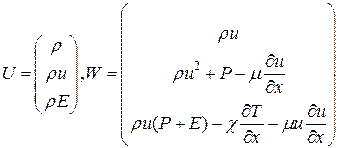
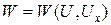 , где
, где 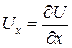 . Схема нелинейная и для построения безытерационной схемы необходимо линеаризовать вектор
. Схема нелинейная и для построения безытерационной схемы необходимо линеаризовать вектор 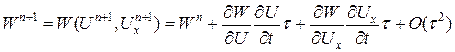 .
. и используя матрицы Якоби, имеем:
и используя матрицы Якоби, имеем: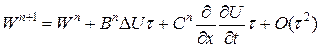 . Здесь матрица
. Здесь матрица 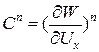 .
.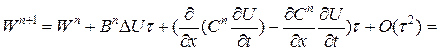
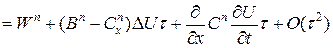 . Здесь матрица
. Здесь матрица  .
. используется разностный оператор
используется разностный оператор , где
, где  .
. .
.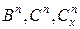 можно упростить, если в качестве искомых переменных выбирать вектор состояния не в массовых переменных, а один из векторов с газодинамическими переменными, например
можно упростить, если в качестве искомых переменных выбирать вектор состояния не в массовых переменных, а один из векторов с газодинамическими переменными, например  . В этом случае легче ставятся граничные условия и уменьшается число арифметических операций при реализации схемы.
. В этом случае легче ставятся граничные условия и уменьшается число арифметических операций при реализации схемы.


