Разностные методы решения уравнений
Основные понятия теории разностных схем Одним из методов изучения физических задач является их численное моделирование. Ниже рассмотрены конечно-разностные методы решения задач гидроаэродинамики исследованных ранее моделей. Определим основные понятия теории разностных схем. Для аппроксимации первых производных введем следующие разностные операторы: оператор правой разности Для аппроксимации пространственной производной второго порядка используем разностный оператор Замечание. Разностные операторы введены для одномерной задачи. Для общего случая они строятся аналогично. Аппроксимацию исходного уравнения и краевых условий назовем разностной схемой. Для анализа устойчивости разностных схем будем пользоваться спектральным методом. При анализе нелинейных уравнений устойчивость схемы будем проверять для линеаризованных уравнений или уравнений с замороженными коэффициентами. Построение разностных схем начнем со следующих часто встречающихся модельных дифференциальных уравнений (см.[7]):
Здесь Заметим, что два последних уравнения нелинейные.
|

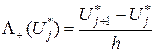 , оператор левой разности
, оператор левой разности  и оператор центральной разности
и оператор центральной разности 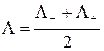 , действующие на сеточную функцию
, действующие на сеточную функцию  , которая определенна на регулярной сетке. Первые два оператора имеют первый, а последний
, которая определенна на регулярной сетке. Первые два оператора имеют первый, а последний 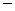 второй порядки точности и аппроксимируют пространственные производные.
второй порядки точности и аппроксимируют пространственные производные. , а временная производная
, а временная производная  . Если индекс «
. Если индекс «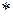 » заменяется на номер «n», то схема является явной, а если
» заменяется на номер «n», то схема является явной, а если 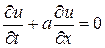 , (19)
, (19)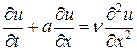 , (20)
, (20)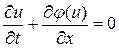 , (21)
, (21)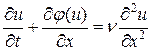 . (22)
. (22)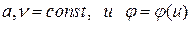 .
.


