Краевые условия для задач внешнего обтекания
При рассмотрении краевых условий будем ориентироваться на задачу обтекания тела потоком жидкости или газа в приближении уравнений газовой динамики, полных и упрощенных уравнений Навье – Стокса (см.[6]). Рассматривается в пространстве X система непересекающихся тел поверхностями: В начальный момент в
включающая замыкающие соотношения, справедлива в области Для полной математической формулировки задачи необходимо задать краевые условия. 1. Если пространство X неограниченно, то на бесконечности задается условие равномерности потока:
В практических расчетах область интегрирования Для сверхзвуковых течений при больших числах Рейнольдса за внешнюю границу может быть выбрана область ударного перехода. На ней задаются обычные или обобщенные условия Ренкина-Гюгонио. 2. Для уравнений Навье-Стокса краевые условия для компонент скорости на поверхности тела
Для термодинамических величин один из режимов теплообмена: распределение температур В случае уравнений газовой динамики, когда эффекты вязкости и теплопроводности не учитываются, граничное условие на поверхности S есть условие непроницаемости тела по нормали: 3. В качестве граничных условий в следе за телом (на выходной границе) берутся приближенные мягкие условия:
Указанные краевые условия являются простейшими вариантами заданий краевых условий. Контрольные вопросы к первой главе: 1. Написать систему уравнений вязкого сжимаемого теплопроводного газа. 2. Перейти к недивергентной форме записи одномерной системе уравнений Навье – Стокса в переменных: а) в) 3. Построить линеаризованную модель системы уравнений Навье – Стокса. 4. Построить параболизированную модель системы уравнений Навье – Стокса. 5. Вывести систему уравнений Прандтля для ламинарного течения. 6. Понятие критериев подобия. Числа Рейнольдса и Маха. 7. Простейшие физические процессы. 8. Иллюстрация применимости физических моделей на примере сверхзвукового обтекания тела.
Практическое задание к первой главе: 1. Используя метод Эйлера, получите уравнение неразрывности в цилиндрических и сферических координатах. 2. Преобразуйте уравнение неразрывности 3. На йдите местное число Маха, соответствующее относительной скорости
|

 , которые могут как покоиться, так и двигаться. Пусть
, которые могут как покоиться, так и двигаться. Пусть 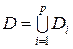 и
и 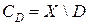 . Тела ограниченны кусочно-гладким
. Тела ограниченны кусочно-гладким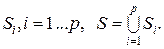
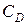 задано начальное состояние потока.
задано начальное состояние потока.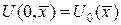 . Будем предполагать, что система:
. Будем предполагать, что система: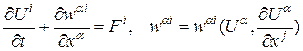 ,
, .
.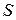 ставятся как условия прилипания:
ставятся как условия прилипания: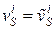 , где
, где  – скорость движения соприкасающейся точки потока и
– скорость движения соприкасающейся точки потока и 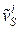 – скорость движения точки поверхности.
– скорость движения точки поверхности. , либо тепловой поток
, либо тепловой поток  , либо общее условие теплообмена
, либо общее условие теплообмена 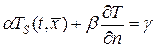 , где
, где 
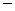 функции от
функции от  и параметров потока.
и параметров потока.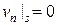 .
. , задающие непрерывность потоков (или векторов состояния) или их производных.
, задающие непрерывность потоков (или векторов состояния) или их производных. ; б)
; б)  ;
; .
. к виду
к виду 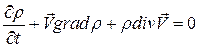 .
. . (М=4, 567)
. (М=4, 567)


