Определители
Матрица (2) называется квадратной, если число строк этой матрицы равно числу столбцов. Порядок квадратной матрицы определяется числом строк (столбцов). Любой квадратной матрице А становится в соответствие некоторое число, называемое определителем или детерминантом этой матрицы, обозначаемое D, или det A, или символом Пусть А – квадратная матрица второго порядка:
Пример 4. Вычислить определитель второго порядка: Решение.
Определители 3-го порядка считаются по правилу Саррюса (правилу треугольника):
= а 11 а 22 а 33 + а 21 а 32 а 13 + а 12 а 23 а 31 – а 31 а 22 а 13 – а 32 а 23 а 11 – а 21 а 12 а 33.
Схематически это правило можно записать так:
Пример 5. Вычислить определитель третьего порядка, используя правило Саррюса:
Решение.
Для вычисления определителей удобно использовать следующие свойства определителей: 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером. Это свойство называется транспонированием. 2. При перестановке двух строк или столбцов определитель меняет знак на противоположный. 3. Если все элементы какой-либо строки или столбца равны нулю, то определитель равен нулю. 4. Если определитель имеет два одинаковых столбца или две одинаковых строки, то он равен нулю. 5. Общий множитель элементов строки или столбца можно выносить за знак определителя. 6. Определитель, у которого элементы одной строки или столбца пропорциональны элементам другой строки или столбца, равен нулю. 7. Величина определителя не изменится, если ко всем элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и то же число.
Определение 1. Минором Mij элемента aij определителя порядка n называется определитель (n – 1) порядка, получающийся из данного путем вычеркивания i строки и j столбца.
Определение 2. Алгебраическим дополнением Aij элемента aij определителя D называется его минор, взятый со знаком (–1) i + j, т.е. Aij = (–1) i + j × Mij. (5)
Пример 6. Найти миноры и алгебраические дополнения для элементов а 32 и а 23 определителя третьего порядка
А 32 = (–1)3 + 2 × М 32 = (–1) × 1 = –1.
А 23 = (–1)2 + 3 × М 23 = (–1) × (–19) = 19.
Сформулируем теорему Лапласа, которая дает возможность вычислить определитель любого порядка. Теорема Лапласа. Определитель D равен сумме произведений элементов какой-либо строки или столбца на их алгебраическое дополнение.
= а 11 А 11 + а 12 А 12 + а 13 А 13 = а 12 А 12 + а 22 А 22 + а 32 А 32. (6)
Пример 7. Вычислить определитель, используя теорему Лапласа:
Решение. Определитель D удобно вычислить, разложив его по элементам третьей строки.
Очевидно, что разложение определителя выгодно производить по строке или столбцу, где содержится больше всего нулей.
Пример 8. Вычислить определитель: Решение. Разложим определитель по элементам 2-й строки:
Чтобы получить как можно больше элементов равных нулю в какой-либо строке или столбце, используем свойство определителя: Если ко всем элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на любое число, то величина определителя не изменяется. Пример 9. Вычислить определитель: Решение. Сделаем в первом столбце все элементы нулевыми, кроме одного. Вторую строку оставим без изменения. Затем элементы второй строки умножим на (–3) и, прибавив к соответствующим элементам первой строки, получим:
Умножим элементы второй строки на 2 и прибавим к элементам третьей строки:
Умножим элементы второй строки на (–1) и прибавим их к элементам четвертой строки. Искомый определитель преобразуется к виду:
Разложив этот определитель по элементам первого столбца, получим:
Для вычисления полученного определителя третьего порядка в третьем столбце сделаем еще один элемент нулевым. Прибавим вторую строку к первой:
Разложив этот определитель по элементам третьего столбца, получим:
|

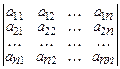 .
. . Для вычисления определителей 2-го порядка справедлива формула:
. Для вычисления определителей 2-го порядка справедлива формула: . (3)
. (3)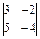
 .
. (4)
(4)
 .
.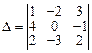 = 1 × 0 × 2 + 4 × (–3) × 3 + (–2) × (–1) × 2 – 2 × 0 × 3– – 4 × (–2) × 2 – 1 × (–3) × (–1) = 0 – 36 + 4 – 0 + 16 – 3 = –19.
= 1 × 0 × 2 + 4 × (–3) × 3 + (–2) × (–1) × 2 – 2 × 0 × 3– – 4 × (–2) × 2 – 1 × (–3) × (–1) = 0 – 36 + 4 – 0 + 16 – 3 = –19. .
.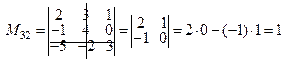


 .
.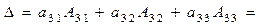
 .
. .
.

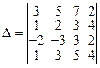 .
. .
. .
. .
. .
. .
. .
.


