Системы линейных уравнений. Метод Гаусса
Рассмотрим систему уравнений:
Такая система называется системой m линейных уравнений с n неизвестными. Решением системы (1) называется совокупность значений неизвестных х 1 = a 1, х 2 = a 2, ¼, хn = a n, которая при подстановке обращает все уравнения в тождества. Если система (1) имеет хотя бы одно решение, то она называется совместной. Если система (1) не имеет ни одного решения, то она называется несовместной. Совместная система линейных уравнений называется определенной, когда она имеет только одно решение, в противном случае система называется неопределенной. Две или несколько систем линейных уравнений называются эквивалентными, если каждое решение одной системы является решением другой системы или каждая из систем несовместна. Элементарными преобразованиями системы уравнений (1) называются такие преобразования, которые, состоят в выполнении следующих действий: 1) перестановка местами любых двух уравнений; 2) умножение обеих частей какого-либо уравнения на число, не равное нулю; 3) прибавление к одному из уравнений системы другого уравнения, умноженного на некоторое число, не равное нулю; 4) удаление из системы уравнений вида 0 × х 1 + 0 × х 2 +¼ + 0 × хn = 0. Каждое из этих преобразований переводит систему в эквивалентную ей. Идея метода Гаусса заключается в том, что последовательным применением преобразований 1) – 4) неизвестное х 1 исключается из всех уравнений системы, кроме первого. После этого первое уравнение в дальнейших операциях не участвует. Применяя затем элементарные операции ко 2-му, 3-му и т.д. m -му уравнениям преобразованной системы, исключаем х 2 из всех этих уравнений, кроме второго. Затем элементарные преобразования применяются к 3-му, 4-му, ¼, m -му уравнениям полученной на предыдущем этапе системы и т.д. Такой процесс эквивалентных преобразований над системой уравнений (1) называется методом Гаусса. При решении системы линейных уравнений методом Гаусса удобно записывать лишь матрицу, составленную из коэффициентов при неизвестных и свободных членов:
Вместо действий над уравнениями производим те же самые операции над строками матрицы. В результате преобразований возможны следующие три случая. I случай. Система (1) сводится к треугольному виду: каждое последующее уравнение содержит на одно неизвестное меньше, чем предыдущее, а последнее уравнение имеет только одно неизвестное. Решая систему снизу вверх, получим ответ. В этом случае система совместна и определена. Пример 1. Найти решение системы уравнений методом Гаусса:
Решение. Вместо действий над уравнениями производим те же самые операции над строками матрицы, из коэффициентов при неизвестных и столбца свободных членов. Для удобства поменяем первую и вторую строки матрицы местами. Преобразования над строками матрицы равносильны преобразованиям над уравнениями системы.
1-й шаг. Первое уравнение (первую строку) оставляем без изменения, а из остальных уравнений исключаем х 1. Для этого первое уравнение умножаем на (–4) и складываем со вторым, затем первое уравнение умножаем на (–3) и складываем с третьим, и первое уравнение умножаем на (–2) и складываем с четвертым. В результате получается следующая матрица:
2-й шаг. Первое и второе уравнения оставляем без изменений, а из третьего и четвертого уравнений исключаем х 2. Для этого второе уравнение умножаем на (–1) и складываем с третьим, затем второе уравнение умножаем на (–7) и складываем с четвертым, умноженным на 5. Получаем матрицу:
3-й шаг. Первое, второе и третье уравнения оставляем без изменений, а из четвертого исключаем х 3. Умножим третье уравнение на (–33) и сложим с четвертым. Запишем получившуюся матрицу:
4-й шаг. Сократим последнюю строку на 135. По полученной матрице запишем систему уравнений:
Получили систему треугольного вида. Используя обратный ход метода Гаусса, найдем из четвертого уравнения х 4 = 1. Подставляя значение х 4 в третье уравнение, найдем х 3: – х 3 – 8 = –5, х 3 = –3. Подставляя значения х 4 и х 3 во второе уравнение, найдем х 2: 5 х 2 –27 +17 = –5, х 2 = 1. Аналогично из первого уравнения найдем х 1 = 2. Ответ: (2; 1; –3; 1), т.е. система совместна и определена.
II случай. В результате преобразований получаем уравнение, левая часть которого равна нулю, а правая не равна нулю; это свидетельствует о несовместимости системы. Пример 2. Решить систему методом Гаусса.
Решение. Составим матрицу. Эквивалентность системы уравнений будем обозначать знаком
В третьем уравнении (оно соответствует 3-й строке) пришли к противоречивому результату: 0 = –8 Ответ: система не имеет решений, т.е. система несовместна.
III случай. Система (1) преобразуется к трапецеидальному виду, т.е. получаем систему у которой число уравнений меньше числа неизвестных. Пример 3. Решить систему методом Гаусса.
Решение. Составим матрицу и проделаем элементарные преобразования. Удобно первое и второе уравнения поменять местами:
Сократим третье уравнение на 2, а четвертое на 3:
Отбросим нулевую строку и по полученной матрице запишем систему уравнений:
Получаем систему трапецеидального вида. Оставим в левой части столько неизвестных, сколько уравнений в системе, т.е. х 1, х 2, х 3, а х 4 перенесем в правую часть.
х 4 – свободное неизвестное, которое может принимать любые значения. Пусть х 4 = n; тогда х 2 = –1 – 5 х 4 + 7 х 3 = –1 – 5 n +5 n +1 = 0. х 1 = –3 x 2 – 5 x 3 + 3 + 2 x 4;
Ответ: Найдем хотя бы одно из них. Пусть n = 1, тогда Ответ:
|

 (1)
(1)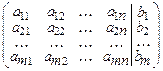 . (2)
. (2) .
. .
. .
. .
. .
.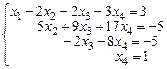 .
.
 . Преобразования над уравнениями для краткости будем записывать символами.
. Преобразования над уравнениями для краткости будем записывать символами.
 ¥
¥ 
 ¥ ¥
¥ ¥  .
. .
.
 ¥
¥  .
.
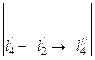 ¥
¥  .
. .
.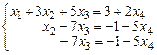 .
. ;
; .
. , система совместна и неопределена, т.е. она имеет бесчисленное множество решений.
, система совместна и неопределена, т.е. она имеет бесчисленное множество решений.



 .
.


