Сложение векторов и умножение вектора на число1. Если
Если a × 3. Признаком коллинеарности векторов
Пример 1. Даны точки А (3, 1, 4), В (–1, 0, 6). Найти координаты вектора Решение. Координаты вектора
Пример 2. Даны векторы Решение. Используя правила действия с векторами, заданными своими координатами (формулы (7), (8)), получим: 2 3
Пример 3. Найти направляющие косинусы вектора Решение. Вектор
Используя формулу (4), получим:
Используя формулу (5), можно проверить правильность ответа:
следовательно, задача решена верно. Пример 4. Даны векторы Решение. Используя признак коллинеарности векторов (формула (9)), запишем отношения координат следующим образом:
Следовательно, векторы
|
= (x 1, y 1, z 1), 
= (x 2, y 2, z 2), то
= (x 1 ± x 2, y 1 ± y 2, z 1 ± z 2). (7)
, то для любого числа α имеем:
или 
. (9)
и его модуль.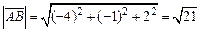
.
.
= 2 
– 3 
+ 2 
.
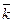. Его координаты равны: х = 5, y = –3, z = 2, т.е.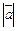 
= 
.
; 
; 
.
+ 
,
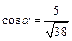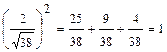