Скалярное произведение векторов. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Обозначается скалярное произведение символом
где j – угол между Свойства скалярного произведения: 1. ( 2. 3. (λ 4. ( 5. Если векторы Если векторы ( Косинус угла φ между векторами
Если векторы заданы координатами, то необходимое и достаточное условие перпендикулярности векторов примет вид: x 1 × x 2 + y 1 × y 2 + z 1 × z 2 = 0, (13) Скалярное произведение векторов ( Отсюда легко находится проекция одного вектора на другой:
Пример 5. Векторы Решение. Используя формулу (10) и свойства скалярного произведения, имеем: ((2
( Следовательно, ((2 Пример 6. Найти угол между векторами Решение. Используем формулу (11). Найдем скалярное произведение векторов
Найдем модули
Подставив найденные значения в формулу (12), получим:
Используя формулу (15) и полученные вычисления, имеем
|

 ×
×  или (
или ( , (10)
, (10) ) = (
) = (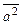 =
=  2.
2. (12)
(12)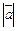 ×
×  =
=  . (14)
. (14) ;
; 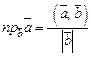 . (15)
. (15) . Зная,
. Зная,  ,
,  , вычислить скалярное произведение вектора
, вычислить скалярное произведение вектора  + 3
+ 3  ) на вектор (
) на вектор ( 2 = 2
2 = 2  2 + (
2 + ( 2 = 52 = 25;
2 = 52 = 25; = 5.
= 5. .
. и
и  .
. ;
; .
. ,
,  .
.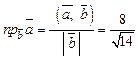 .
.


