а) неравенство  можно записать так: –2 <
можно записать так: –2 < 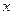 – 3 < 2. К каждой части этих неравенств прибавим по 3 и получим:
– 3 < 2. К каждой части этих неравенств прибавим по 3 и получим:
–2 + 3 < х < 2 + 3, т.е. 1 < х < 5.
б) в случае неравенства

имеем

и

, т.е.

и

.
2.5.4. Определение предела функции в точке.
Геометрический смысл предела функции
Определение. Пусть функция  определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция
определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция  стремится к пределу
стремится к пределу  (
( ) при
) при 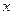 , стремящемся к а (
, стремящемся к а ( , если для каждого положительного числа
, если для каждого положительного числа  , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число  , что для всех
, что для всех 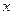 , отличных от а и удовлетворяющих неравенству
, отличных от а и удовлетворяющих неравенству  , имеет место неравенство
, имеет место неравенство  .
.
Если  есть предел функции
есть предел функции  при
при  , то пишут:
, то пишут:
 или
или  и при
и при  .
.
Рассмотрим геометрический смысл предела функции в точке.
Если  при
при  , то на графике функции
, то на графике функции  это иллюстрируется следующим образом (рис.7).
это иллюстрируется следующим образом (рис.7).
Рис. 7
Из неравенства  или
или  следует неравенство
следует неравенство  или
или  , это значит, что для всех точек х, отстоящих от точки
, это значит, что для всех точек х, отстоящих от точки  не далее чем на d, точки графика функции у = f (x) лежат внутри полосы шириной 2 e, ограниченной прямыми
не далее чем на d, точки графика функции у = f (x) лежат внутри полосы шириной 2 e, ограниченной прямыми 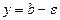 и
и 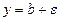 .
.
2.5.5. Бесконечно малые величины и их свойства
Определение. Функция a = a (х) называется бесконечно малой при  или при
или при  , если
, если  или
или  .
.
Свойства бесконечно малых функций:
1. Если функции a (х) и b (х) бесконечно малые при  (или
(или  ), то их алгебраическая сумма a (х) ± b (х) бесконечно мала при
), то их алгебраическая сумма a (х) ± b (х) бесконечно мала при  (или
(или  ).
).
Это утверждение распространяется на любое конечное число бесконечно малых функций.
2. Если при  (или
(или  ) функция a (х) бесконечно малая, а функция j (х) ограничена, то их произведение
) функция a (х) бесконечно малая, а функция j (х) ограничена, то их произведение  – бесконечно малая функция при
– бесконечно малая функция при  (или
(или  ).
).
3. Если a (х) ® 0 при  (или
(или  ) и не обращается в нуль, то
) и не обращается в нуль, то  .
.
4. Частное от деления a (х) на функцию j (х), предел которой не равен нулю, есть величина бесконечно малая.
2.5.6. Бесконечно большие величины и их свойства
Определение. Функция f (x) называется бесконечно большой при  , если имеет место одно из равенств:
, если имеет место одно из равенств:
 ,
, 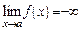 .
.
 имеем
имеем  и
и  , т.е.
, т.е.  и
и  .
.

 можно записать так: –2 <
можно записать так: –2 < 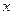 – 3 < 2. К каждой части этих неравенств прибавим по 3 и получим:
– 3 < 2. К каждой части этих неравенств прибавим по 3 и получим:
 определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция
определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция  (
( ) при
) при  , если для каждого положительного числа
, если для каждого положительного числа  , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число  , что для всех
, что для всех  , имеет место неравенство
, имеет место неравенство  .
. есть предел функции
есть предел функции  при
при  , то пишут:
, то пишут: или
или  и при
и при 
 следует неравенство
следует неравенство  или
или  , это значит, что для всех точек х, отстоящих от точки
, это значит, что для всех точек х, отстоящих от точки  не далее чем на d, точки графика функции у = f (x) лежат внутри полосы шириной 2 e, ограниченной прямыми
не далее чем на d, точки графика функции у = f (x) лежат внутри полосы шириной 2 e, ограниченной прямыми 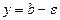 и
и 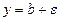 .
. или при
или при  , если
, если  или
или  .
. (или
(или  ).
). – бесконечно малая функция при
– бесконечно малая функция при  .
. , если имеет место одно из равенств:
, если имеет место одно из равенств: ,
, 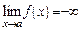 .
.


