Решение. . ?имер 13. Вычислить данные пределы, используя формулу (41): 1) ; 2) ; 3) ; 4) ; 5) ; 6) .1) 2) 3)
4)
5)
6)
Второй замечательный предел заключается в следующем. В случае, когда при х ® ¥ функция f (x) представляет степень, основание которой стремится к единице, а показатель к бесконечности, для нахождения предела функции используется второй замечательный предел:
Число е – иррациональное. Его значение с десятью верными знаками после запятой: е = 2, 7182818284…
Пример 13. Вычислить данные пределы, используя формулу (41):
Решение. Прежде чем применить второй замечательный предел, надо убедиться, что при х ® ¥ основание стремится к единице. 1)
2)
3)
4) Разделим числитель и знаменатель на х.
Вычислим отдельно предел числителя и знаменателя.
Следовательно,  .
5) т.е. применить второй замечательный предел нельзя. При х ® ¥ мы имеем 2 в бесконечно большой степени, это бесконечно большая величина, т.е.
6) При х ® ¥
2.5.10. Непрерывность функций
|
.
.
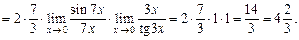
. (41)
;
;
;
;
;
.
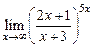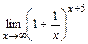, найдем 
, (
– бесконечно малая величина при х ® ¥).
; 
,
.
; 
,
; 
.
.
, 
,
.
, 
.
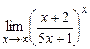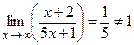в степени х будет бесконечно малой величиной, а предел бесконечно малой величины равен нулю, т.е.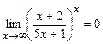 
.
