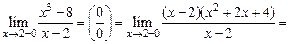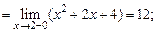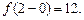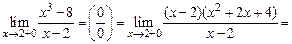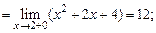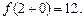Если отыскивается предел функции  при условии, что х, стремясь к
при условии, что х, стремясь к  , может принимать только такие значения, которые больше
, может принимать только такие значения, которые больше  , то этот предел, если он существует, называется правосторонним пределом функции
, то этот предел, если он существует, называется правосторонним пределом функции  . То, что
. То, что  , стремясь к
, стремясь к  , остается больше
, остается больше  , обозначается
, обозначается  , а правосторонний предел функции обозначается одним символом
, а правосторонний предел функции обозначается одним символом  или
или  .
.
Пример 16. Найти односторонние пределы функции
 при
при  слева и справа.
слева и справа.
Решение. Задача сводится к нахождению двух пределов:  и
и  .
.
Если 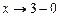 , т.е.
, т.е.  , оставаясь меньше 3, то величина
, оставаясь меньше 3, то величина  является бесконечно малой, принимающей отрицательные значения. Обратная ей величина будет бесконечно большой, принимающей также отрицательные значения, тем же свойством обладает и величина
является бесконечно малой, принимающей отрицательные значения. Обратная ей величина будет бесконечно большой, принимающей также отрицательные значения, тем же свойством обладает и величина  , поэтому
, поэтому  .
.
Если  , т.е.
, т.е.  , оставаясь больше 3, то величина х – 3 является положительной бесконечно малой. Обратная ей величина
, оставаясь больше 3, то величина х – 3 является положительной бесконечно малой. Обратная ей величина  будет бесконечно большой, принимающей положительные значения. Этим свойством обладает и величина
будет бесконечно большой, принимающей положительные значения. Этим свойством обладает и величина  , поэтому
, поэтому  .
.
Пример 17. Найти односторонние пределы функции  при
при  слева и справа.
слева и справа.
Решение. Найдем значение двух пределов:  и
и  .
.
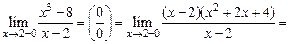
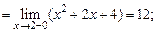
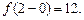
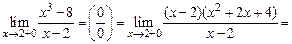
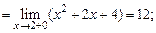
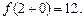

 при условии, что х, стремясь к
при условии, что х, стремясь к  , может принимать только такие значения, которые больше
, может принимать только такие значения, которые больше  , стремясь к
, стремясь к  , а правосторонний предел функции обозначается одним символом
, а правосторонний предел функции обозначается одним символом  или
или  .
. при
при  слева и справа.
слева и справа. и
и  .
.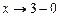 , т.е.
, т.е.  является бесконечно малой, принимающей отрицательные значения. Обратная ей величина будет бесконечно большой, принимающей также отрицательные значения, тем же свойством обладает и величина
является бесконечно малой, принимающей отрицательные значения. Обратная ей величина будет бесконечно большой, принимающей также отрицательные значения, тем же свойством обладает и величина  , поэтому
, поэтому  .
. , т.е.
, т.е.  будет бесконечно большой, принимающей положительные значения. Этим свойством обладает и величина
будет бесконечно большой, принимающей положительные значения. Этим свойством обладает и величина  , поэтому
, поэтому  .
. при
при  слева и справа.
слева и справа. и
и  .
.