Основные правила дифференцирования
Если u и v – функции независимой переменной x: u = u (x) и 1. Производная постоянной равна нулю, т. е. если y = c, то 2. Постоянный множитель можно выносить за знак производной, т. е. если 3. Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций, т. е. если 4. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную от второй функции, т. е. если 5. Производная дроби (т.е. частного от деления двух функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, т.е. если 6. Производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по х, т.е. если
|

 .
.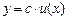 , то
, то  .
.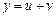 , то
, то 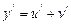 .
.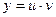 , то
, то  .
. , то
, то 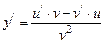 .
.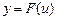 и
и 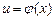 , то
, то  .
.


