Предел дробно-рациональной функции
Если
т.е. при отыскании предела дробно-рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, если при этом предельном значении знаменатель не обращается в нуль.
Пример 2. Найти Решение. В данном случае мы имеем дробно-рациональную функцию. Прежде чем применить формулу (39), надо проверить, не обращается ли в нуль знаменатель дроби при х = 3. Проверяем:
Пример 3. Найти Решение. Найдем значение знаменателя дроби при х = 1, имеем:
Используем формулу (39).
Если аргумент стремится к бесконечности или к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования. Путем рассуждений, основанных на свойствах пределов, можно записать часто встречающиеся пределы (постоянная а > 0): 1. 2. 3. 4. Этими простейшими пределами можно пользоваться как формулами. Раскрытие неопределенности вида Чтобы раскрыть неопределенность вида Пример 4. Найти Решение. Подставив непосредственно то значение х, к которому оно стремится, видим, что имеем случай Делим числитель и знаменатель дроби на х 3 (наивысшая степень х), находим При х ® ¥ Пример 5. Найти Решение. При х ® ¥ имеем неопределенность
Так как при х ® ¥ Пример 6. Найти Решение. Разобрав полученные результаты последних трех пределов, можно сформулировать следующие правила вычисления предела при х ® ¥ в случае 1) предел частного двух многочленов при х ® ¥ равен 2) предел частного двух многочленов при х ® ¥ равен 0, если степень числителя меньше степени знаменателя. 3) предел частного двух многочленов при х ® ¥ равен отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Раскрытие неопределенности вида Правило 1. Для того чтобы определить предел дробно-рациональной функции в случае, когда при х ® а числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разложить на простые множители, сократить на Пример 7. Найти Решение. При х = 1 числитель и знаменатель обращаются в нуль, получается неопределенность вида
Правило 2. Чтобы найти предел дроби, содержащей иррациональные выражения, когда предел числителя и знаменателя дроби при х ® а равен нулю, надо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель, сделать необходимые упрощения и перейти к пределу.
Пример 8. Найти Решение. При х = 3 числитель и знаменатель дроби обращаются в нуль. Избавимся от иррациональности в знаменателе, умножая числитель и знаменатель на
Пример 9. Найти Решение. При х = 0 числитель и знаменатель дроби обращаются в нуль. Избавимся от иррациональности в числителе, умножая числитель и знаменатель на
Раскрытие неопределенности вида (¥ – ¥) Этот случай нахождения предела функции можно привести к случаю Пример 10. Найти Решение. При х = 2 функция представляет разность двух положи-тельных бесконечно больших величин (случай (¥ – ¥)). Произведем вычитание дробей и сделаем преобразования.
Пример 11. Найти Решение. При х ® ¥ выражение, стоящее в скобках, есть разность двух бесконечно больших величин. Умножим и разделим функцию, стоящую под знаком предела, на выражение, сопряженное с
При х ® ¥ знаменатель дроби, стоящей под знаком предела, есть функция бесконечно большая (как сумма двух бесконечно больших величин), поэтому дробь
|

 то
то если
если  , (39)
, (39)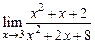 .
.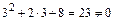 ,
, .
. .
.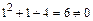 .
. .
. .
. .
.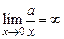 .
.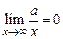 .
.
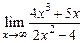 .
. .
. ,
,  и
и  являются бесконечно малыми. Следовательно, в числителе мы имеем число, близкое к 4, а в знаменателе – бесконечно малое, их отношение будет бесконечно большой величиной, т.е. предел равен ¥.
являются бесконечно малыми. Следовательно, в числителе мы имеем число, близкое к 4, а в знаменателе – бесконечно малое, их отношение будет бесконечно большой величиной, т.е. предел равен ¥.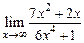 .
. .
. ,
,  и
и 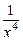 бесконечно малы, то их предел при х ® ¥ равен 0.
бесконечно малы, то их предел при х ® ¥ равен 0.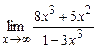 .
. .
. , если степень числителя больше степени знаменателя.
, если степень числителя больше степени знаменателя.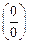
 .
. . Преобразуем данную функцию, разлагая на множители числитель и знаменатель по формуле ах 2 + bх + с =
. Преобразуем данную функцию, разлагая на множители числитель и знаменатель по формуле ах 2 + bх + с =
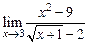 .
. . Получаем:
. Получаем: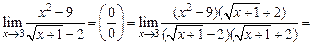

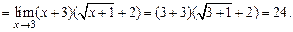

 :
:

 .
.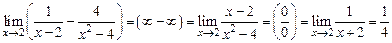 .
.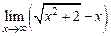 .
. , т.е. на
, т.е. на  . Получим:
. Получим:

 есть величина бесконечно малая. Предел бесконечно малой величины равен нулю.
есть величина бесконечно малая. Предел бесконечно малой величины равен нулю.


