Введение в математический анализ
Дать ответы на теоретические вопросы: 1. Определение функции. 2. Способы задания функции. 3. Основные элементарные функции. 4. Абсолютная величина действительного числа. Окрестность точки. 5. Определение предела функции в точке. 6. Геометрический смысл предела функции. 7. Бесконечно малые величины и их свойства. 8. Бесконечно большие величины и их свойства. 9. Основные теоремы о пределах. 10. Вычисление пределов. 11. I и II замечательные пределы. 12. Непрерывность функции. 13. Односторонние пределы. 14. Точки разрыва и их классификация.
2.5.1. Определение функции. Способы задания функции Если каждому значению переменной х, принадлежащему некоторой области, соответствует одно определенное значение другой переменной у, то у есть функция от х, или в символической записи Переменная х называется независимой переменной или аргументом. Зависимость переменных х и у называется функциональной зависимостью. Функция у = f (х) может быть задана табличным, графическим или аналитическим способом. Табличный способ состоит в том, что функция задается таблицей, содержащей значение аргумента х и соответствующее значение функции f (х). Графический способ – это совокупность точек плоскости (хоу), абсциссы которых являются независимой переменной, а ординаты –соответствующими значениями функции. Эта совокупность точек называется графиком данной функции. Аналитический способ – это задание функции формулой вида
2.5.2. Основные элементарные функции Основными элементарными функциями называют аналитическим способом заданные функции. 1. Степенная функция: у = хn, где n – действительное число. 2. Показательная функция: у = ах, где а – положительное число, не равное единице (а > 0, a ¹ 1). 3. Логарифмическая функция: у = log ax, где основание логарифма а – положительное число, не равное единице (а > 0, a ¹ 1). 4. Тригонометрические функции: у =sin x, у =cos x, у =tg x, у =ctg x, у =sec x, у =cosec x. 5. Обратные тригонометрические функции: у =arcsin x, у =arccos x, у =arctg x, у =arcctg x, у =arcsec x, у =arccosec x. Функции, заданные одной формулой посредством конечного числа арифметических действий и операций, определяемых основными элементарными функциями, называются элементарными. Например: Все остальные функции называются неэлементарными. Например, неэлементарной является функция, определяемая несколькими различными формулами для различных интервалов изменения аргумента:
2.5.3. Абсолютная величина действительного числа Определение. Абсолютной величиной (или модулем) действительного числа х (обозначается
Например: Если
неравенствам 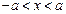 , (рис.4). , (рис.4).
Рис.4
Если  , то отсюда следует, что , то отсюда следует, что  и и  (рис.5). (рис.5).
Рис.5
Решениями неравенства 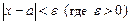 будут точки будут точки 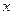 интервала (а – e, а + e) (рис.6), удовлетворяющие неравенству интервала (а – e, а + e) (рис.6), удовлетворяющие неравенству а – e < х < а + e. Рис.6 Всякий интервал, содержащий точку а, называется окрестностью точки а. Интервал (а – e, а + e), т.е. множество точек
Пример 1. Определить, при каких значениях х будут справедливы следующие неравенства: а)
|

 = f (x),
= f (x), 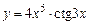 ;
;  и т.д.
и т.д. .
.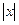 ) называется неотрицательное действительное число, удовлетворяющее следующим условиям:
) называется неотрицательное действительное число, удовлетворяющее следующим условиям:

 , это означает, что х удовлетворяет
, это означает, что х удовлетворяет


 (где e > 0), называется e окрестностью точки а.
(где e > 0), называется e окрестностью точки а. б)
б)  .
.


