Решение. а) Так как прямая параллельна прямой х = 3 + 6t, y = 2 – 4t, z = 7 – t, то они имеют один и тот же направляющий вектор
а) Так как прямая параллельна прямой х = 3 + 6 t, y = 2 – 4 t, z = 7 – t, то они имеют один и тот же направляющий вектор б) В качестве направляющего вектора можно взять вектор в) Поскольку вектор
Пример 15. Составить канонические уравнения прямой, проведенной через точку М 0(6, 2, –3) параллельно вектору Решение. Применив формулу (16), получим канонические уравнения прямой: Подставим в эти уравнения координаты точки А (2, 7, –10).
Проверим, лежит ли точка В (10, –3, 5) на прямой
Пример 16. Найти уравнения прямой, проходящей через точки Решение. Согласно формуле (34), имеем:
Пример 17. Найти острый угол между двумя прямыми
Решение. Зная направляющие векторы прямых
Пример 18. Найти проекцию точки А (1, –3, 2) на плоскость Решение. Проекцией точки А на плоскость будет точка пересечения данной плоскости и перпендикуляра к этой плоскости, проходящего через точку А. Нормальный вектор плоскости х = 1 + 6 t, y = –3 + 3 t, z = 2 – t. Подставляя значения х, у, z в уравнение плоскости, найдем значение параметра t: 6 × (1 + 6t) + 3× (–3 + 3t) – 1 × (2 – t) = 0, отсюда t = 1. Подставляя значения t = 1 в параметрические уравнения прямой, найдем координаты искомой точки (проекции): х = 7, у = 0,
|

 . Подставляя значения х 0 = 5, у 0 = –1; z 0 = –4 и координаты вектора
. Подставляя значения х 0 = 5, у 0 = –1; z 0 = –4 и координаты вектора  в формулы (32), (33) получим уравнения искомой прямой
в формулы (32), (33) получим уравнения искомой прямой 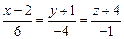 и
и 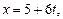

 ;
;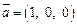 , соответствующий орт-вектор
, соответствующий орт-вектор  , тогда имеем
, тогда имеем 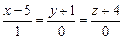 и
и 

 .
. перпендикулярен плоскости
перпендикулярен плоскости  и
и 

 .
. . Лежат ли на этой прямой точки А (2, 7, –10) и В (10, –3, 5)?
. Лежат ли на этой прямой точки А (2, 7, –10) и В (10, –3, 5)? .
. , следовательно, точка А лежит на прямой.
, следовательно, точка А лежит на прямой. , точка В не принадлежит прямой.
, точка В не принадлежит прямой. или
или  .
.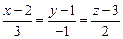 и
и 
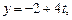
 .
.
 .
. = (6, 3, –1) будет направляющим вектором для прямой. Параметрическое уравнение этой прямой:
= (6, 3, –1) будет направляющим вектором для прямой. Параметрическое уравнение этой прямой:


