Решение.
1. 2. 3. 4.
Пример 2. Найти действительную и мнимую части числа:
Решение. Будем выполнять преобразования последовательно. 1. (–2 + 4 i)× (3 – i) = –6 + 12 i + 2 i – 4 i 2 = –6 + 14 i + 4 = –2 + 14 i. 2. (–2 – 2 i)2 = (–2)2 + 2× (–2)(–2 i) + (–2 i)2= 4 + 8 i + 4 i 2 = 8 i. 3. 4. i 18 = i 16 × i 2 = (i4)4 × i 2 = 1 × (–1)= –1. 5. Ответ: Пример 3. Найти x и y и записать комплексное число z, если (2 x + 3 i)(–1 + i) – (2 x + iy)(–3 i) = 4 + 2 i. Решение. Преобразуем левую часть: (2 x + 3 i)(–1 + i) – (2 x + iy)(–3 i) = = –2 x + 3 i + 2 xi + 3 i 2 + 6 xi + 3 yi 2 = = –2 x – 3 i + 2 xi – 3 + 6 xi –3 y = = (–2 x – 3 y –3) + i (8 x – 3). Получим: (–2 x – 3 y – 3) + i (8 x – 3) = 4 + 2 i. Используя равенство комплексных чисел, запишем систему уравнений:
Пример 4. Решить уравнение z 2 – 2 z + 4 = 0. Решение.
1.5.3. Тригонометрическая форма комплексного числа Комплексное число в тригонометрической форме имеет вид
где r – модуль комплексного числа z и обозначается | z |,
угол j называется аргументом числа z и обозначается Arg z. Из значений j = arg z выделяется главное значение arg z, удовлетво-ряющее условию  . .
Пример 5. Представить в тригонометрической форме следующие комплексные числа: Решение. Чтобы представить в тригонометрической форме комплексное число, надо: 1) построить точку на комплексной плоскости, соответствующую данному комплексному числу; 2) провести радиус-вектор этой точки; 3) найти модуль комплексного числа z; 4) найти аргумент числа z. При вычислении аргумента комплексного числа z необходимо учитывать четверть, в которой лежит точка z.
2) Рассмотрим z 2 = –1 + i.
3) Рассмотрим z 3 = –1 – i.
4)
5)
6) Рассмотрим z 6 = – 3 = –3 + 0 i.
.
7) Рассмотрим z 7 = 2 i = 0 + 2 i.
. 8)
.
1.5.4. Действия над комплексными числами Над комплексными числами в тригонометрической форме удобно выполнять следующие действия: умножение, деление, возведение в степень, извлечение корня. Пусть комплексные числа заданы в тригонометрической форме:
Тогда модуль произведения этих числе равен произведению модулей сомножителей, а аргумент произведения – сумме аргументов сомножителей:
Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя:
Если Пусть n – целое положительное число, а
где k = 0, 1, ¼, n – 1. Если k давать n, (n + 1), ¼, значения, то будут повторяться значения корня при k = 0, 1, ¼, n – 1.
1.2.5. Показательная форма комплексного числа По формуле Эйлера
Пусть комплексные числа заданы в показательной форме:
Тогда: 1) 2) 3) 4)
Пример 6. Комплексные числа z 1 = –2 + 2 i,
Решение. Представим z 1= –2 + 2 i в тригонометрической форме:
Представим
1) Найдем z = z 1 × z 2.
2)
3)
4)
Получаем три значения корня: k 1 = 0, k 2 = 1,
k 3 = 2,
Ответ каждого примера можно записать в показательной форме: 1) z 1 × z 2 = 2) 3) 4) КОНТРОЛЬНая РАБОТа №2
|

 = (3 – 4 i) + (–5 +2 i) = (3 – 5) + i (–4 + 2) = –2 – 2 i.
= (3 – 4 i) + (–5 +2 i) = (3 – 5) + i (–4 + 2) = –2 – 2 i. = (3 – 4 i) – (–5 – 2 i) = (3 – (–5)) + i (–4 – (–2)) = 8 – 2 i.
= (3 – 4 i) – (–5 – 2 i) = (3 – (–5)) + i (–4 – (–2)) = 8 – 2 i. = (3 – 4 i)(–5 +2 i) = 3× (–5) + (–4 i)× (–5) + 3× 2i + (–4 i)× (2 i) =
= (3 – 4 i)(–5 +2 i) = 3× (–5) + (–4 i)× (–5) + 3× 2i + (–4 i)× (2 i) =
 .
.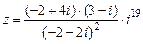 .
. .
. .
.
 .
. .
. т.к. i 2 = –1, а
т.к. i 2 = –1, а  , имеем
, имеем  ,
, 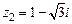 .
.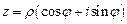 ,
, ,
,
 z =
z = 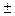 3; z =
3; z =  1) Рассмотрим комплексное число z 1 = 1 + i. На комплексной плоскос-ти построим точку М 1 с координатами (1; 1), соответствующую этому числу, проведем радиус-вектор и отметим угол j 1.
1) Рассмотрим комплексное число z 1 = 1 + i. На комплексной плоскос-ти построим точку М 1 с координатами (1; 1), соответствующую этому числу, проведем радиус-вектор и отметим угол j 1.










 Рассмотрим z 4 = 1 – i.
Рассмотрим z 4 = 1 – i.



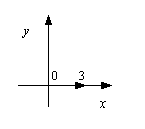 Рассмотрим z 5 = 3 = 3 + 0 i.
Рассмотрим z 5 = 3 = 3 + 0 i.








 Рассмотрим z8 = – 2 i = 0 – 2 i.
Рассмотрим z8 = – 2 i = 0 – 2 i.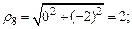


 .
. .
.
 . Эта формула называется формулой Муавра.
. Эта формула называется формулой Муавра. ,
,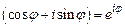 . Следовательно, всякое комплексное число можно еще представить в показательной форме. В этом случае оно имеет следующий вид:
. Следовательно, всякое комплексное число можно еще представить в показательной форме. В этом случае оно имеет следующий вид: .
. ,
,  .
.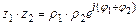 ;
; ;
; ;
; , k = 0, 1, 2 ¼, (n – 1) × V.
, k = 0, 1, 2 ¼, (n – 1) × V. представить в тригонометрической форме. Найти:
представить в тригонометрической форме. Найти:

 .
.



 .
.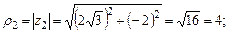


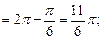

 ;
; ;
; ;
;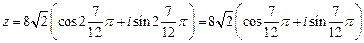 .
.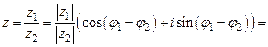






 , k = 0, 1, 2.
, k = 0, 1, 2. ;
;

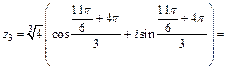






 .
.


