Решение. 1) Так как матрица А квадратная, она может иметь обратную
1) Так как матрица А квадратная, она может иметь обратную. 2) Найдем определитель матрицы А:
т.к. 3) Строим матрицу АТ, транспонированную матрице А. 4) Каждый элемент матрицы АТ заменяем его алгебраическим дополнением:
5) В формулу (9) подставим найденные значения.
6) Сделаем проверку.
1.4.3. Решение систем линейных уравнений средствами матричного исчисления Матричным способом решаются квадратные системы линейных уравнений, т.е. системы, у которых число уравнений равно числу неизвестных, и определитель, составленный из коэффициентов при неизвестных, не равен нулю.
Пример 16. Решить систему уравнений матричным способом.
Решение. Обозначим через А матрицу из коэффициентов при неизвестных:
Тогда систему в матричном виде можно записать следующим образом: АХ = В. Сделаем преобразования:
Найдем матрицу, обратную матрице А. Вычислим определитель матрицы А:
(Определитель посчитан по правилу треугольников). Так как Запишем матрицу, транспонированную матрице А:
Составим матрицу
Обратная матрица имеет вид Проверка
Запишем решение системы:
Получили Ответ: (–1; 2; 3), система совместна и определена.
|
,
, матрица А имеет обратную.
.
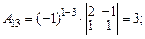
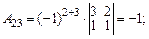
, полученная матрица А –1 является обратной матрице А.
= 
.
.
.
; через Х матрицу-столбец из неизвестных:
и через В –матрицу-столбец из свободных членов 
.
.
.
из алгебраических дополнений матрицы АТ.
.
.
.
.
= 
. Если две матрицы одинаковой размерности равны, то равны все их соответствующие элементы, т.е. х 1= –1; х 2= 2; х 3= 3.
