Матрицы
Матрицей размера m ´ n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу называются элементами матрицы. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, ¼, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: аij, где i – номер строки, j – номер столбца. Кроме круглых скобок, для обозначения матрицы используются [ ], || ||. Матрица размера n ´ n называется квадратной:
Главной диагональю квадратной матрицы называется диагональ, составленная из элементов а 11, а 22, ¼, аnn. Диагональной матрицей называется квадратная матрица, у которой все элементы, не находящиеся на главной диагонали, равны нулю:
Единичной матрицей называется диагональная матрица, у которой каждый элемент, находящийся на главной диагонали, равен единице:
Нулевой матрицей называется матрица, все элементы которой нули. Матрица размера m ´ 1 называется матрица столбец.
Матрица размера 1 ´ n называется матрица строка.
1.4.1. Алгебра матриц 1. Две матрицы называются равными, если они одинакового размера и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. 2. Суммой двух матриц А и В одного и того же размера m ´ n будет третья матрица С размера m ´ n, элементы которой равны сумме соответствующих элементов матриц А и В. 3. Произведением матрицы А размера m ´ n на число l будет матрица С того же размера m ´ n, элементы которой равны соответствующим элементам матрицы А, умноженным на число l. 4. Произведением матрицы Аm ´ k × Bk ´ n называется такая матрица Сm´ n, каждый элемент которой сij равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй.
Пример 11. Найти матрицу С = 2А + 3В, если
Решение. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число. Следовательно:
Чтобы сложить (вычесть) две матрицы одинаковой размерности, надо сложить (вычесть) их соответствующие элементы.
Пример 12. Найти матрицу С = АТ + 2 В, если:
Решение. Строим матрицу АТ, транспонированную матрице А, для чего в матрице А строки и столбцы поменяем местами.
Пример 13. Найти произведение матрицы А × В и В × А, если Решение. Матрицы можно перемножить только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. У матрицы А три столбца, у матрицы В три строки, следовательно, произведение А × В существует. Произведение В × А также возможно, т.к. у матрицы В два столбца, а у матрицы А две строки. Произведением матрицы А размера m
А × В
Пример 14. Найти значение многочлена f (A) от матрицы А, если f (x) = 3 x 2 – 4, Решение. f (A) = 3 А 2 – 4 Е. Где Е – единичная матрица. Найдем А 2.
1.4.2. Обратная матрица Определение 1. Квадратная матрица А называется вырожденной, если det A = 0, и невырожденной, если det A ¹ 0. Определение 2. Матрица А –1 называется обратной для матрицы А, если А × А –1 = А –1 × А = Е, (8) где Е –единичная матрица.
Теорема. Всякая невырожденная матрица А имеет обратную матрицу вида:
где Аij – алгебраические дополнения элемента аij матрицы А. Правило построения обратной матрицы: 1) Находим det A. Если det A ¹ 0, то матрица А невырожденная и для нее существует обратная. Если det A = 0, то матрица А вырожденная и обратная матрица А –1 не существует. 2) Находим матрицу АТ, транспонированную к матрице А. 3) Заменяем каждый элемент матрицы АТ его алгебраическим дополнением, используя формулу (5). 4) Вычисляем обратную матрицу по формуле (9). 5) Проверяем правильность вычисления обратной матрицы, используя формулу (8).
Пример 15. Найти матрицу А –1 обратную матрице А, если
|

 .
. .
. .
. .
.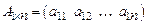 .
.
 .
.
 .
.
 .
.
 .
.
 ,
, .
. ,
,  .
. n на матрицу В размера n
n на матрицу В размера n 
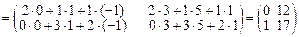

 ;
; В А.
В А. .
. ;
; 
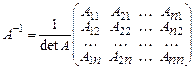 , (9)
, (9) .
.


