Аналитическая геометрия
Дать ответы на теоретические вопросы: 1. Определение линии в аналитической геометрии. 2. Нахождение точки пересечения двух линий. 3. Общее уравнение прямой на плоскости. 4. Что называется угловым коэффициентом прямой на плоскости? 5. Уравнение прямой с угловым коэффициентом. 6. Угол между двумя прямыми. 7. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом. 8. Уравнение прямой, проходящей через две данные точки на плоскости. 9. Признаки параллельности и перпендикулярности прямых на плоскости. 10. Определение нормального вектора плоскости. 11. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор. 12. Общее уравнение плоскости. 13. Уравнение плоскости, проходящей через три заданные точки. 14. Условие параллельности и перпендикулярности двух плоскостей. 15. Направляющий вектор прямой. 16. Канонические уравнения прямой в пространстве. 17. Параметрические уравнения прямой в пространстве. 18. Канонические уравнения прямой, проходящей через две данные точки. 19. Условия параллельности и перпендикулярности двух прямых в пространстве. 2.4.1. Прямая линия на плоскости Прямая линия на плоскости определяется уравнением первой степени, и, наоборот, каждое уравнение первой степени определяет прямую. Уравнение вида: Ах + Ву + с = 0 (16) называется общим уравнением прямой. Уравнение у = kх + b (17)
называется уравнением прямой с угловым коэффициентом, где k – угловой коэффициент, равный тангенсу наклона прямой к оси Ох, т.е. k = tg a; b – величина отрезка, который отсекает прямая на оси Оу, считая от начала координат (рис. 1). Рис.1 Уравнение у – у 0 = k (х – х 0) (18) называется уравнением прямой, проходящей через точку М 0(х 0, у 0) с угловым коэффициентом k. Если прямая проходит через точки М 1(х 1, у 1) и М 2(х 2, у 2), то ее уравнение определяется по формуле:
Уравнение прямой
называется уравнением прямой в отрезках, где а и b – длины отрезков, отсекаемые на осях координат, взятые с соответствующими знаками. Если прямые заданы уравнениями у = k 1 х + b 1 и у = k 2 х + b 2, то тангенс угла между ними определяется формулой:
Признаком параллельности двух прямых является равенство их угловых коэффициентов: k 1 = k 2. (22) Признаком перпендикулярности двух прямых является соотношение: k 1 × k 2= –1 или Если прямые заданы общими уравнениями: А 1 х + В 1 у + С 1 = 0 и А 2 х + В 2 у + С 2 = 0, (24) то условие перпендикулярности прямых можно записать в следующем виде: А 1 × А 2 + В 1 × В 2 = 0, а условие параллельности:
При рассмотрении уравнений прямых(24) можно представить три случая: а) б) с)
Пример 1. Построить прямую 2 х – 3 у +6 = 0. Решение. Определим точки пересечения прямой 2 х – 3 у +6 = 0 с координатными осями; при у = 0 получаем 2 х + 6 = 0, х = –3. Точка А пересечения прямой с осью Ох имеет координаты (–3; 0); при х = 0 имеем –3 у + 6 = 0, у = 2, и прямая пересекает ось Оу в точке В (0; 2). Построим эти точки, соединим их прямой и получим прямую, соответствующую данному уравнению (рис.2).
Пример 2. Построить прямую у = –2 х. Решение. Прямая у = –2 х проходит через начало координат (b = 0), поэтому для построения достаточно найти только одну точку, принадлежащую ей. Взяв х = –1, получим у = –2 × (–1) = 2, т.е. Пример 3. Найти угловой коэффициент прямой Решение. Уравнение прямой дано в общем виде. Уравнение прямой с угловым коэффициентом имеет вид у = kх + b. Решим уравнение прямой 4 х – 3 у + 12 = 0 относительно у: 3 у = 4 х + 12, у = Следовательно, угловой коэффициент k = Пример 4. Под каким углом прямая у = 2 х + 3 пересекает ось Ох? Решение. Прямая задана уравнением с угловым коэффициентом в виде (2), следовательно, k = 2. Т.к. k – это тангенс угла, который прямая составляет с положительным направлением оси Ох, то можно записать: k = tg φ = 2, т.е. tg φ = 2, а φ = arctg2.
Пример 5. Найти уравнение прямой, проходящей через две точки М 1(–1, 2) и М 2(2, 1). Решение. В уравнении (19), полагая х 1 = –1, у 1 = 2, х 2 = 2, у 2 = 1, получим Пример 6. Найти уравнение прямой, проходящей через точку Решение. Так как угловые коэффициенты параллельных прямых между собой равны, а для данной прямой
Пример 7. Найти уравнение прямой, проходящей через точку А (5, –1) перпендикулярно к прямой 3 х – 7 у +14 = 0. Решение. Угловой коэффициент искомой прямой найдем из формулы (23), т.е. он должен быть обратен по абсолютной величине и противоположен по знаку угловому коэффициенту данной прямой. Угловой коэффициент данной прямой 3 х – 7 у +14 = 0, Подставив координаты точки А (5, –1) и значение Сделав преобразования, получим общее уравнение прямой: 7 у – 4 х – 26 = 0.
Пример 8. Найти точку пересечения прямых х – 3 у + 11 = 0 и 9 х + 7 у – 3 = 0. Решение. Прямые заданы общими уравнениями. Чтобы найти точку их пересечения, надо решить систему:
Следовательно, прямые пересекаются в точке А (–2; 3).
2.4.2. Плоскость в пространстве Плоскость в пространстве относительно прямоугольной системы координат может быть задана различными способами. В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость. Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение плоскости, проходящей через данную точку А (х – х 0) + В (у – у 0) + С (z – z 0) = 0. (25) Раскрывая в уравнении (25) скобки и обозначая число Ах + Ву + Сz + D = 0. (26) Уравнение (26) называется общим уравнением плоскости. Частные случаи общего уравнения плоскости: 1. Свободный член D равен нулю, т.е. Ах + Ву + Сz = 0 (плоскость проходит через начало координат). 2. Один из коэффициентов при текущих координатах равен нулю и а) D А = 0, Ву + Сz + D = 0 (плоскость параллельна оси Ох); В = 0, Ах + Сz + D = 0 (плоскость параллельна оси Оу); С = 0, Ах + Ву + D = 0 (плоскость параллельна оси Оz); б) D = 0, тогда плоскость проходит через соответствующую координатную ось: А = 0, Ву + Сz = 0 (плоскость проходит через ось Ох); В = 0, Ах + Сz = 0 (плоскость проходит через ось Оу); С = 0, Ах + Ву = 0 (плоскость проходит через ось Оz). 3. Два коэффициента при текущих координатах равны нулю и а) D В = 0, С = 0, ах + D = 0 (плоскость параллельна плоскости Оуz); А = 0, С = 0, Ву + D = 0 (плоскость параллельна плоскости Охz); А = 0, В = 0, Сz + D = 0 (плоскость параллельна плоскости Оху); б) D = 0, тогда плоскость совпадает с соответствующей координатной плоскостью: В = 0, С = 0, ах = 0 или х = 0 (уравнение плоскости Оуz); А = 0, С = 0, Ву = 0 или у = 0 (уравнение плоскости Охz); А = 0, В = 0, Сz = 0 или z = 0 (уравнение плоскости Оху). Если ни один из коэффициентов общего уравнения (26) не равен нулю, то оно может быть преобразовано к виду
где Уравнение (27) называется уравнением плоскости в отрезках. Уравнение плоскости, проходящей через три данные точки М 1(х 1, у 1, z 1), М 2(х 2, у 2, z 2) и М 3(х 3, у 3, z 3), в координатной форме имеет вид:
Угол между двумя плоскостями
Необходимое и достаточное условие параллельности плоскостей:
Условие перпендикулярности плоскостей: А 1 × А 2 + В 1 × В 2 + С 1 × С 2 = 0. (31)
Пример 9. Составить уравнение плоскости, перпендикулярной вектору Решение. Подставляя в уравнение (25) значения А = 2, В = –1, С = 4, х 0 = 5, у 0 = 2, z 0 = –3, получим 2(х – 5) – (у – 2) + 4(z + 3) = 0. Раскрывая скобки и приводя подобные члены, находим искомое уравнение плоскости 2 х – у + 4 z + 4 = 0. Пример 10. Определить отрезки, отсекаемые плоскостью Решение. Переписав уравнение в виде 2 х – 3 у + 8 z = 4 и разделив обе его части на 4, получим:
Сравнивая последнее уравнение с уравнением (27), находим а = 2;
Пример 11. Составить уравнение плоскости, проходящей через три данные точки М 1(1, 3, –2), М 2(4, –5, 6) и М3(–3, 1, 2). Решение. Уравнение плоскости, проходящей через точки М 1, М 2 и М 3, в соответствии с (28), запишется так:
Разлагая определитель по элементам первой строки, получим
или после преобразования имеем 8 х + 22 у + 19 z – 36 = 0.
Пример 12. Найти угол между плоскостями: 11 х – 8 у – 7 z +5 = 0 и 7 х + 2 у – 8 z – 3 = 0. Решение. Подставляя в формулу (29) значения А 1 = 11, В 1 = –8,
Следовательно, φ = 450.
Пример 13. Через точку М (2, –1, –3) провести плоскость, параллельную плоскости 5 х – 4 у + 6 z –3 = 0. Решение. Из уравнения данной плоскости запишем координаты ее нормального вектора 5(х –2) + (–4) × (у – (–1)) + 6 (z – (–3)) = 0, 5 х – 4 у + 6 z + 4 = 0. 2.4.3. Прямая в пространстве Прямая в пространстве относительно прямоугольной декартовой системы координат может быть задана различными способами. Например, прямая однозначно определяется точкой и параллельным ей вектором, двумя точками и т.д. В зависимости от способа задания прямой рассматривают различные виды ее уравнений. Прямая как пересечение двух плоскостей определяется совместным заданием двух уравнений первой степени:
при условии, что коэффициенты А 1, В 1, С 1 первого из них не пропорциональны коэффициентам А 2, В 2, С 2. Каждый не равный нулю вектор, лежащий на данной прямой или параллельной ей, называется направляющим вектором этой прямой. Если известна одна точка М 0(х 0, у 0, z 0), прямой и направляющий вектор
В этом случае уравнения прямой называются каноническими. Обозначив буквой t каждое из равных отношений в канонических уравнениях, мы получим параметрические уравнения прямой, проходящей через точку М 0(х 0, у 0, z 0) с направляющим вектором:
Канонические уравнения прямой, проходящей через две данные точки М 1(х 1, у 1, z 1) и М 2(х 2, у 2, z 2), имеют вид:
Если в пространстве заданы две прямые:
а) условие параллельности этих прямых:
б) условие перпендикулярности:
в) угол между прямыми определяется по формуле:
Пример 14. Составить канонические и параметрические уравнения прямых, проведенных через точку М 0(5, –1, –4) в каждом из следующих случаев: a) прямая параллельна прямой х = 3 + 6 t, y = 2 – 4 t, z = 7 – t; b) прямая параллельна оси Ох; c) прямая перпендикулярна плоскости х + 2 у + 3 z –5 = 0.
|


 . (19)
. (19) (20)
(20) . (21)
. (21) . (23)
. (23) .
. – прямые имеют одну общую точку, чтобы найти ее координаты, надо решить систему уравнений
– прямые имеют одну общую точку, чтобы найти ее координаты, надо решить систему уравнений  ;
;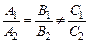 – прямые параллельны;
– прямые параллельны; – прямые сливаются, т.е. оба уравнения определяют одну и ту же прямую.
– прямые сливаются, т.е. оба уравнения определяют одну и ту же прямую.
 х +4.
х +4. , или
, или  . После упрощения получаем уравнение прямой в общем виде у + 3 х – 5 = 0.
. После упрощения получаем уравнение прямой в общем виде у + 3 х – 5 = 0. , то и угловой коэффициент искомой прямой также равен
, то и угловой коэффициент искомой прямой также равен  . Используем уравнение (19), и зная координаты точки А (2, 5), имеем х 0 = 2, у 0 = 5. Подставляя найденные значения в формулу (18), получим:
. Используем уравнение (19), и зная координаты точки А (2, 5), имеем х 0 = 2, у 0 = 5. Подставляя найденные значения в формулу (18), получим: ; 4 у – 3 х – 14 = 0.
; 4 у – 3 х – 14 = 0. ; тогда угловой коэффициент прямой, ей перпендикулярной,
; тогда угловой коэффициент прямой, ей перпендикулярной,  .
.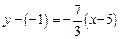 .
. .
. имеет вид:
имеет вид: 0, тогда плоскость параллельна соответствующей координатной оси:
0, тогда плоскость параллельна соответствующей координатной оси: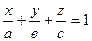 , (27)
, (27)

 – алгебраические величины направленных отрезков, отсекаемых на осях координат.
– алгебраические величины направленных отрезков, отсекаемых на осях координат. . (28)
. (28) и А 2 х + В 2 у + С 2 z + D 2 = 0 определяется формулой:
и А 2 х + В 2 у + С 2 z + D 2 = 0 определяется формулой: . (29)
. (29)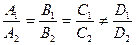 . (30)
. (30) и проходящей через точку М 0(5, 2, –3).
и проходящей через точку М 0(5, 2, –3). или
или  .
.
 .
. или
или  .
.

 .
. . Так как по условию плоскости параллельны, то нормальный вектор данной плоскости может служить нормальным вектором искомой плоскости. Данная задача свелась к примеру 1. Используем формулу (25):
. Так как по условию плоскости параллельны, то нормальный вектор данной плоскости может служить нормальным вектором искомой плоскости. Данная задача свелась к примеру 1. Используем формулу (25): ,
, , то прямая может быть определена уравнениями вида:
, то прямая может быть определена уравнениями вида: . (32)
. (32)
 . (33)
. (33) . (34)
. (34) и
и 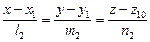 , то:
, то: ; (35)
; (35) ; (36)
; (36) . (37)
. (37)


