Третье определение непрерывности функции в точке
Определение 3. Функция Таким образом, для непрерывности функции в точке
или иначе:
2.5.12. Точки разрыва и их классификация Если равенство (44) в какой-либо его части не выполняется, то о точке Определение 1. Если левосторонний предел функции
то точка х 0 называется точкой разрыва первого рода (рис.9). Рис. 9
Определение 2. Если в точке  не существует левосторонний или правосторонний предел функции или оба одновременно, то эта точка называется точкой разрыва второго рода. не существует левосторонний или правосторонний предел функции или оба одновременно, то эта точка называется точкой разрыва второго рода.
Рис.10 Рис.11 Рис.12
На рис. 10 отсутствует левосторонний предел функции; на рис. 11 нет правостороннего предела функции, а на рис. 12 у функции нет ни левостороннего, ни правостороннего предела. Во всех этих случаях функция в точке
Определение 3. Если в точке  функция f (x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке функция f (x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке  , т.е. со значением f (x), то точка , т.е. со значением f (x), то точка  называется точкой устранимого разрыва (рис. 13). называется точкой устранимого разрыва (рис. 13).
Рис. 13
В этом случае: f (x 0 – 0) = f (x 0 + 0) Разрыв «устраняется» тем, что полагают f (x 0) равным
Пример 18. Исследовать функцию Решение. При х = 2 данная функция не определена, следовательно, она не непрерывна в этой точке, и точка х = 2 является точкой разрыва. Определим характер разрыва. Найдем левосторонний и правосторонний пределы в точке х = 2.
f (2 – 0) = f (2 + 0), но в самой точке х = 2 функция неопределена, следовательно, в точке х = 2 функция терпит устранимый разрыв (46). Графиком данной функции является прямая у = х + 1, из которой выколота точка (2; 3) (рис.14).
Рис. 14 Пример 19. Исследовать на непрерывность функцию Решение. Так как знаменатель дроби обращается в нуль в точке х = –2, то функция терпит разрыв в этой точке. Определим характер разрыва.
f (–2 – 0) = 0, f (–2 + 0) = следовательно, в точке х = –2 функция терпит разрыв второго рода. Чтобы построить график функции, исследуем поведение функции на бесконечности (рис.15).
 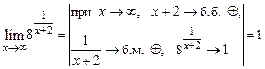
Рис.15
Пример 20. Исследовать на непрерывность функцию Построить график. Решение. Данная функция определена на всей числовой оси, но из этого не следует, что она непрерывна на всей числовой оси. Эта функция неэлементарная, она задана двумя различными формулами для различных интервалов изменения аргумента х и может иметь разрыв в точке х = 2, где меняется ее аналитическое выражение. Исследуя точку х = 2, находим односторонние пределы функции при стремлении аргумента к этой точке слева и справа.
Для удобства исследования сделаем следующий чертеж (рис.16). Рис. 16
Левосторонний и правосторонний пределы конечны, но не равны между собой. Следовательно, функция в точке х = 2 терпит разрыв первого рода (8).
В этой точке разрыва функция имеет конечный скачок: f (2 + 0) – f (2 – 0) = 2 – (–2) = 4. Рис. 17
График функции Пример 21. Найти точки разрыва функции. Если они существуют, указать, какого рода разрыв. Сделать чертеж.
Решение. Неэлементарная функция f (x) определена для всех значений х ³ 0. Она может иметь разрыв в точках х = 1 и х = 2, 5, где меняется аналитическое выражение. Исследуем точки х = 1 и х = 2, 5.
т.к. односторонние пределы имеют конечные значения, но неравны, то в точке х = 2, 5 функция f (х) терпит разрыв I рода. Построим график функции: a) b) у = 4 – 2 х – прямая, лежащая в интервале 1 < х < 2, 5; c)
у = 2 х – 7 – прямая, для которой х ³ 2, 5. График данной функции изображен на рисунке 18. Рис. 18
|

 называется непрерывной при
называется непрерывной при  , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т.е. равны
, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т.е. равны  .
.
 (44)
(44) и ее правосторонний предел
и ее правосторонний предел  существуют, но не равны между собой, т.е. если
существуют, но не равны между собой, т.е. если , (45)
, (45)


 f (x 0). (46)
f (x 0). (46) .
. на непрерывность и построить график.
на непрерывность и построить график. .
.

 , построить график этой функции.
, построить график этой функции.

 ,
,


 ;
; .
.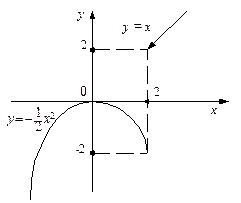
 представляет собой параболу с вершиной в начале координат, ветви которой направлены вниз. Берем ту часть параболы, которая расположена слева от точки х = 2. График функции у = х прямая, проходящая через начало координат. Берем ту часть прямой, которая лежит справа от точки х = 2. Точка х = 2 принадлежит параболе. График данной функции изображен на рис. 17.
представляет собой параболу с вершиной в начале координат, ветви которой направлены вниз. Берем ту часть параболы, которая расположена слева от точки х = 2. График функции у = х прямая, проходящая через начало координат. Берем ту часть прямой, которая лежит справа от точки х = 2. Точка х = 2 принадлежит параболе. График данной функции изображен на рис. 17.
 ;
;  .
. , т.к.
, т.к. 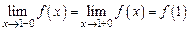 , то в точке
, то в точке 
 ,
, – парабола, расположенная в I четверти в интервале 0 £ х £ 1;
– парабола, расположенная в I четверти в интервале 0 £ х £ 1;



