Касательная и нормаль к плоской кривой
Касательной к кривой
Уравнение касательной к кривой  в точке М 0(х 0, у 0): в точке М 0(х 0, у 0):  . (1) . (1)
Рис. 19
Нормалью к кривой в точке М 0(х 0, у 0) называется прямая, проходящая через М 0 и перпендикулярная к касательной в данной точке (рис. 19). Уравнение нормали к кривой
Примеры. 1. Написать уравнение касательной и нормали к кривой f (x) = x 3 в точке М 0(2, 8). Решение. Точка М 0 принадлежит кривой, это легко увидеть, подставив координаты точки М 0 в уравнение кривой: 8 = 23. Находим производную данной функции и ее значение при Подставляя значения у – 8 = 12(х – 2) или 12 х – у – 16 = 0 – уравнение касательной;
2. Составить уравнение касательной и нормали к параболе Решение. Подставляя в уравнение параболы заданную абсциссу точки касания х 0 = 1, найдем ее ординату: у0 = 12 – 4 × 1 = –3, М0(1, –3). Найдем Подставляя х 0, у 0 и f /(1) в уравнения (1), (2), получим уравнения касательной и нормали: y – (–3) = –2(x – 1) или 2 х + у + 1 = 0.
3.8. Исследование функций и построение их графиков 3.8.1. Возрастание и убывание функций
Функция  называется возрастающей в некотором интервале, если для любых двух чисел х 1 и х 2 из этого интервала из неравенства х 2 > х 1 следует неравенство f (х 2) > f (х 1) (рис.20). называется возрастающей в некотором интервале, если для любых двух чисел х 1 и х 2 из этого интервала из неравенства х 2 > х 1 следует неравенство f (х 2) > f (х 1) (рис.20).
Рис. 20
Если же из неравенства х 2 > х 1 следует нестрогое неравенство f (х 2) Функция f (x) называется убывающей в некотором интервале, если для любых двух чисел х 1 и х 2 из этого интервала из неравенства
Рис. 21
Если же из неравенства х 2 > х 1следует нестрогое неравенство Функции возрастающие и убывающие, а также функции невозрастающие и неубывающие называются монотонными.
Теорема. Если во всех точках некоторого интервала первая производная Эта теорема выражает достаточный признак возрастания и убывания функции на интервале.
Правило. При решении задач, в которых требуется определить интервалы возрастания и убывания функции, следует прежде всего определить область существования этой функции, а затем решить неравенства
Пример 1. Определить интервал возрастания и убывания функции f (x) = x 3 – 12x + 11. Решение. Областью существования данной функции является вся ось Ох (функция существует при любом значении х). Ее производная
Следовательно, функция возрастает в двух бесконечных интервалах: Чтобы определить интервал убывания функции, решим неравенство 3 х 2 –12 < 0 или
Пример 2. Определить интервалы возрастания и убывания функции Решение. Функция
3.8.2. Максимум и минимум (экстремум) функции. Наибольшее Определение максимума. Говорят, что функция Иначе: функция Определение минимума. Говорят, что функция Иначе: функция На рис. 22 изображена функция, определенная на отрезке [ a, b ], которая при х = х 1 и х = х 3 имеет максимум, при х = х 2 и х = х 4 –минимум. Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум, а значение функции в этой точке называется экстремальным.
Рис.22 3.8.3. Необходимое условие экстремума Если функция f (x) имеет экстремум при х = х 0, то ее первая производная в этой точке равна нулю, или ¥, или не существует. Из этого следует, что точки экстремума функции следует разыскивать только среди тех, в которых ее первая производная Точки, в которых первая производная функции равна нулю, бесконечности, а также те, в которых она не существует, называются критическими. Указанный признак экстремума является только необходимым, но не достаточным. Поэтому, определив критические точки, в которых функция может достигать экстремума, надо каждую из точек в отдельности исследовать на основании достаточных условий существования экстремума.
3.8.4. Достаточное условие существования экстремума Если при переходе слева направо через критическую точку первая производная функции меняет знак с плюса на минус, то в этой точке функция достигает максимума. Если при переходе слева направо через критическую точку первая производная меняет знак с минуса на плюс, то в этой точке функция достигает минимума. Если же при переходе через критическую точку первая производная функции не меняет знак, то экстремума нет.
3.8.5. Правило исследования функции на экстремум Для исследования функции на экстремум по первой производной надо: 1. Найти область определения функции. 2. Найти 3. Решить уравнение 4. Все критические точки расположить в порядке возрастания их абсцисс в интервале (a, b).
5. Внутри каждого из интервалов 6. Рассмотреть знаки 7. Найти значение функции в точках, где она достигает экстремума. 3.8.6. Наибольшее и наименьшее значение функции на отрезке Если функция Правило. Чтобы определить наибольшее и наименьшее значения функции на отрезке, надо: 1) определить критические точки функции; 2) вычислить значения функции в критических точках, принадлежащих отрезку [ a, b ] и на концах отрезка [ a, b ]; 3) из полученных значений выбрать наибольшее и наименьшее. Пример 3. Найти экстремум функции
|


 (2)
(2)
 .
.

 в уравнения (1) и (2), получим соответственно:
в уравнения (1) и (2), получим соответственно: или х + 12 у – 98 = 0 – уравнение нормали.
или х + 12 у – 98 = 0 – уравнение нормали. .
. или х – 2 у – 7 = 0.
или х – 2 у – 7 = 0.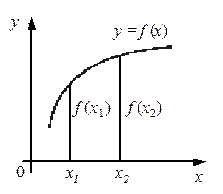
 f (х 1), то функция называется неубывающей в этом интервале.
f (х 1), то функция называется неубывающей в этом интервале.
 , то функция
, то функция  , то функция в этом интервале убывает.
, то функция в этом интервале убывает. . Чтобы найти интервалы возрастания функции, решим неравенство 3 x 2 – 12 > 0.
. Чтобы найти интервалы возрастания функции, решим неравенство 3 x 2 – 12 > 0. т.е.
т.е. 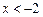 и
и  или
или  .
. , т.е. –2 < x < 2 или
, т.е. –2 < x < 2 или  . Отсюда делаем вывод, что функция убывает в интервале
. Отсюда делаем вывод, что функция убывает в интервале  .
. во всем этом интервале. Поэтому функция
во всем этом интервале. Поэтому функция  максимум, если значение функции в этой точке больше, чем ее значения во всех точках, достаточно близких к
максимум, если значение функции в этой точке больше, чем ее значения во всех точках, достаточно близких к  .
.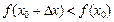 для любых как положительных, так и отрицательных, но достаточно малых
для любых как положительных, так и отрицательных, но достаточно малых  .
. для любых как положительных, так и отрицательных
для любых как положительных, так и отрицательных  , но достаточно малых по абсолютной величине.
, но достаточно малых по абсолютной величине.
 ,
,  или не существует.
или не существует. .
. .
.

 ¼,
¼,  взять любую точку и установить в этой точке знак первой производной функции.
взять любую точку и установить в этой точке знак первой производной функции. непрерывна на отрезке [ a, b ], то на этом отрезке всегда имеются точки, в которых она принимает наибольшее и наименьшее значения. Эти значения функция достигает или в критических точках, или на концах отрезка [ a, b ].
непрерывна на отрезке [ a, b ], то на этом отрезке всегда имеются точки, в которых она принимает наибольшее и наименьшее значения. Эти значения функция достигает или в критических точках, или на концах отрезка [ a, b ]. . Определить ее наибольшее и наименьшее значения на отрезке [–2, 4].
. Определить ее наибольшее и наименьшее значения на отрезке [–2, 4].


